第 2 章 算法原理
本章讲述目前rBAS集成的三种算法,即BAS,BSAS,BSAS-WPT的原理。如有错漏,还请指出。此外,本章所述的算法,在原始的BAS基础上,并没有过多地改变根本上的东西。第3章的算法,则是BAS和其他一些算法的结合,又或者,有更多根本性改动。如王糖糖同学提出的BSO,很典型地BAS和PSO的结合,则不在此章节。
2.1 BAS
关于BAS,主要的参考资料为姜向远博士和李帅老师在arXiv上的论文,BAS: beetle antennae search algorithm for optimization problems。而我是在知乎上看到一篇文章后,才开始复现BAS算法。
2.1.1 算法流程
1.随机生成方向向量,标准化
\[\begin{equation} \overrightarrow{\mathbf{b}}=\frac{\text{rnd}(n,1)}{\|\text{rnd}(n,1)\|} \tag{2.1} \end{equation}\]
其中,\(n\)是待优化参数的维度。
2.计算左右须的坐标
\[\begin{equation} \begin{split} \mathbf{x}_r&=\mathbf{x}^t+d^t\overrightarrow{\mathbf{b}} \\ \mathbf{x}_l&=\mathbf{x}^t-d^t\overrightarrow{\mathbf{b}} \end{split} \tag{2.2} \end{equation}\]
其中,\(\mathbf{x}^t\)为\(t\)时刻天牛的位置,\(d^t\)则是\(t\)时刻,质心到须的距离。
3.根据两须对应函数值,决定天牛下一时刻移动位置
\[\begin{equation} \mathbf{x}^t=\mathbf{x}^{t-1}-\delta^t\overrightarrow{\mathbf{b}}\text{sign}(f(\mathbf{x}_r)-f(\mathbf{x}_l)) \tag{2.3} \end{equation}\]
其中,\(\delta^t\)为t时刻的步长,\(f\)为待优化目标函数。
4.搜索距离与步长更新
\[\begin{align} d^t&= \eta_d d^{t-1}+d_0 \tag{2.4}\\ \delta^t&=\eta_{\delta} \delta^{t-1} \tag{2.5} \end{align}\]
其中,\(d_0\)是人为设定的距离的常数,\(\eta_d\)与\(\eta_\delta\)分别是搜索距离和步长的更新衰减系数。
为了避免参数过多,姜向远博士在BAS-WPT算法中是按照式(2.6)来更新搜索距离和步长的。其中,\(c_2\)是人为设定的常数。
\[\begin{equation}
\begin{split}
\delta^t&=\eta_{\delta} \delta^{t-1}\\
d^t &= \frac{\delta^t}{c_2}\\
\end{split}
\tag{2.6}
\end{equation}\]
2.1.2 收敛性分析
章节2.1.2来源于文章(Zhang Yinyan 2019).
本章节中对BAS算法收敛性进行了分析。首先给出收敛性的定义。
收敛性分析基于definition 2.1进行的。在分析之前,为便于解释,记 \(\mathbf{f}^k_{bst}=\min_{\mathbf{x}^j}\{f(\mathbf{x}^j)\}\) ,其中,\(j=0,1,\cdots,k\) 以及 \(f^k_{bst}=f(\mathbf{x}^k_{bst})\).
引理 2.1给出了一个确定性的结论,即BAS算法在长期看来是不会发散的。
Proof. 假设已经合理设置了BAS算法的参数,在每个时刻\(k\),\(P_\Omega(\mathbf{x}^k+\delta^k\mathbf{b}~\text{sgn}(f(\mathbf{x}^k_r)-f(\mathbf{x}^k_l)))\) 处于最小化\(f\)优化问题的最优解 \(\mathbf{x}^*\)上的概率要大于0。\(P_\Omega(\cdot)\) 表示在\(\Omega\)上的投影。令\(p_k\)表示在时刻\(k\)时,\(\mathbf{x}^k\)不处于最优解\(\mathbf{x}^*\)上的概率。 然后,我们可以得到
\[\begin{equation*} p(\mathbf{x}^k_{bst}=\mathbf{x}^*)>=1-p_0p_1\cdots p_k. \end{equation*}\]
注意,在上面的假设中,我们可知 \(0\leq p_k<1\) . 因此, \[\begin{equation*} \lim_{k\rightarrow+\infty} (1-p_0p_1 \cdots p_k )= 1- \lim_{k\rightarrow+\infty} p_0p_1 \cdots p_k = 1. \end{equation*}\]
注意到 \[p(\mathbf{x}^k_{bst}=\mathbf{x}^*)\leq1.\] 因此,通过夹逼定理,我们进一步地得到 \[\lim_{t\rightarrow+\infty} p(\mathbf{x}^k_{bst}=\mathbf{x}^*) =1.\]
证明完成。定理2.1展示了,通过合理地选择步长,我们能保证BAS算法是依概率1渐进收敛的。
这个结论很重要。第一,该结论展示了BAS算法能在给定的某个步长下收敛。第二,当面对一个确定的函数时,这个定理能帮助我们来判断为什么BAS算法不能有一个好的解。这也是绝大多数仿生算法都会存在的问题。
2.1.3 不足与改进
在对BAS算法的复现与案例应用中,我个人认为,其可能存在如下的缺点。
- 步长更新策略(反馈)
- 缺点:无论每一步得到的结果是否变得更优,步长总会衰减;
- 改进:带有反馈的步长更新,在无法找到更优的位置时,才进行步长的更新;
- 初始步长选取(参数标准化)
- 缺点:对于多参数且量纲相差较大的问题,步长 \(\delta\) 的初始值并不好选取;
- 改进:标准化参数后,再进行调节,这也是
BAS-WPT的技巧所在;
- 群体寻优
- 缺点:1只天牛在随机方向上搜索更优的位置,容易迷失;
- 改进:多只天牛寻优,设定的回合内无法找到更优位置,再考虑步长更新;
- 约束处理能力不足
- 缺点:在约束边界上优化目标突变问题的处理上表现不佳
- 改进:二阶
BAS
2.2 BSAS
在2.1.3节中提及,BAS可能在步长更新和群体寻优两个方面的策略上有一定的不足。因此,我比较莽撞地改出一个粗糙的算法,那就是所谓的BSAS,即beetle swarm antennae search。在BSAS: Beetle Swarm Antennae Search Algorithm for Optimization Problems中,我给出了更为详细的材料。至于具体和王甜甜同学的BSO,即beetle swarm optimization有何不同,我需要进一步研究她的论文材料。
2.2.1 与BAS不同之处
此部分没有公式,因为和BAS算法核心公式思路是一致的。而图2.1与图2.2描述了一种假设的寻优场景,能比较清晰地体现BSAS与BAS之间的不同。
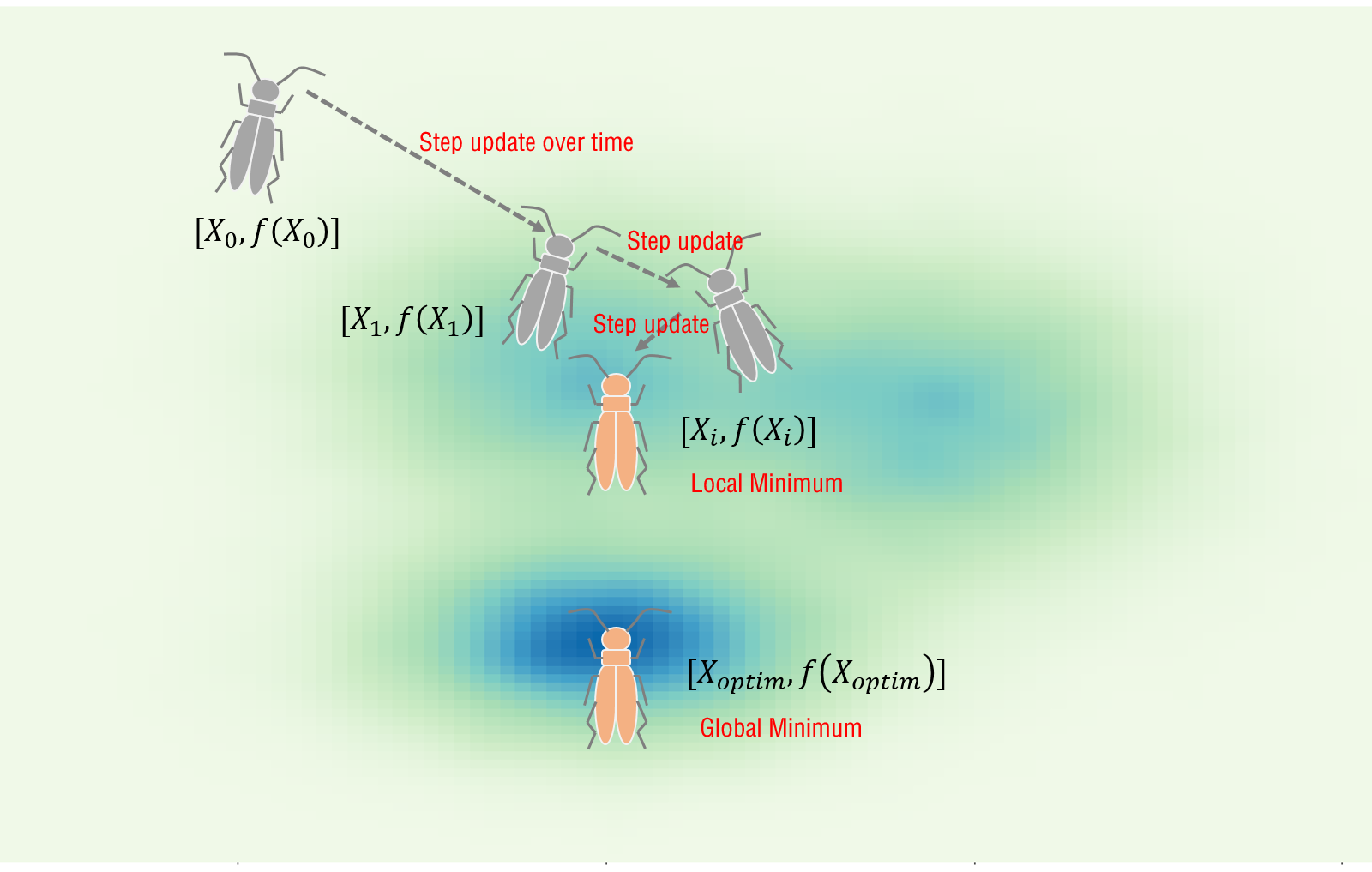
图 2.1: BAS寻优过程示意
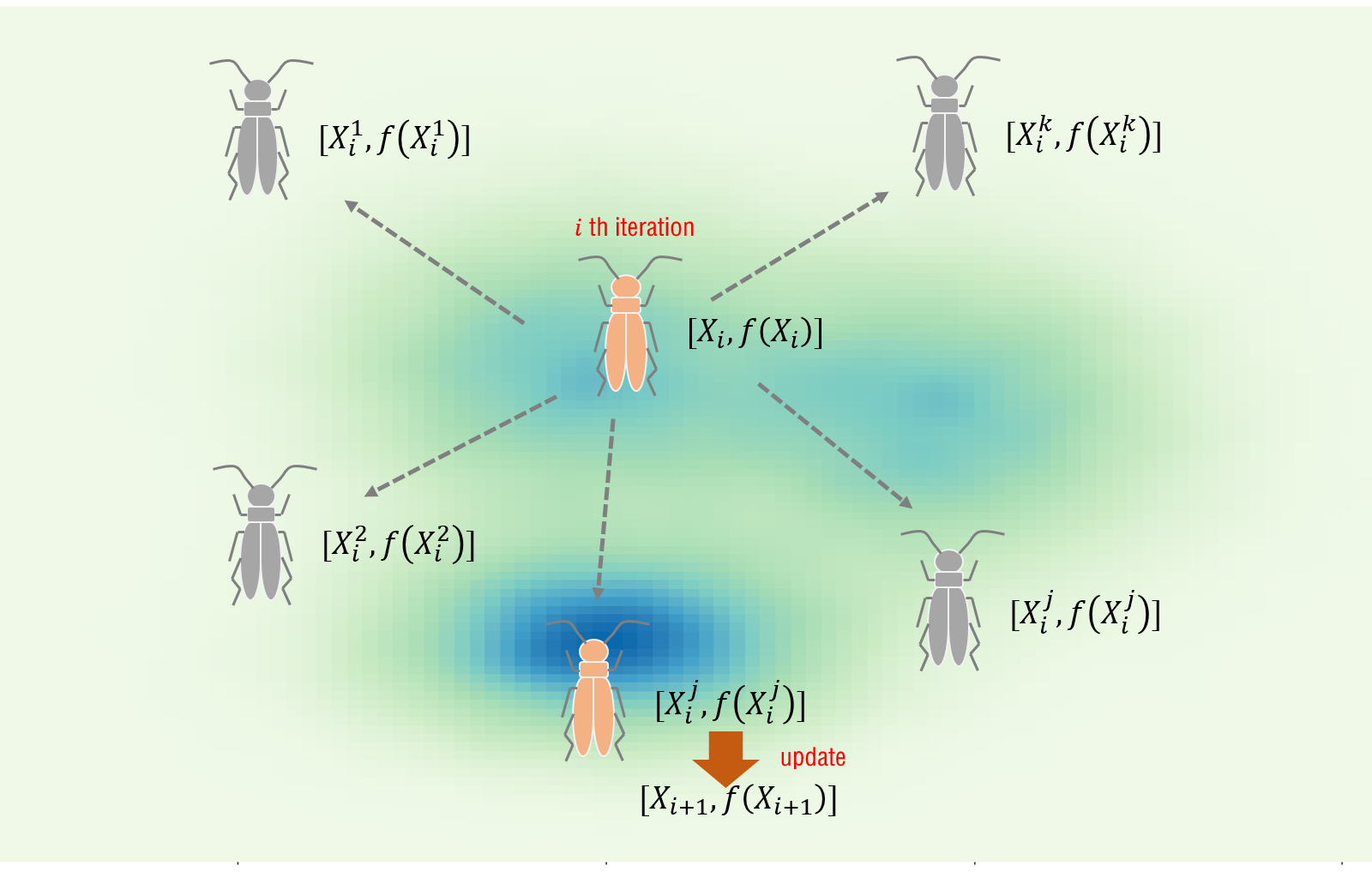
图 2.2: BSAS寻优过程示意
假定,天牛要找到图中最蓝的点。图2.1 中,天牛的起点在距离最优点较远处。由于位置更新只与时间有关,也就是每一步,天牛的步长都会缩减(为了可视化效果,天牛的大小我并没有缩放)。如果初始位置距离最优点较远,那在给定的步长缩减情况下,天牛只能在一个局部最优点处收敛。而图2.2中,每回合天牛会派出\(k\)只天牛在外试探,如果有更优的点,那么更新天牛位置。这样天牛可以更好地到达全局最优点。
2.2.2 不足与改进
虽然解决了步长更新和群体寻优的策略问题,但是还有两点并未解决。
- 初始步长选取(参数标准化)
- 缺点:对于多参数且量纲相差较大的问题,步长 \(\delta\) 的初始值并不好选取;
- 改进:标准化参数后,再进行调节,这也是
BAS-WPT的技巧所在;
- 约束处理能力不足
- 缺点:在约束边界上优化目标突变问题的处理上表现不佳
- 改进:二阶
BAS
好的是,在rBAS 0.1.5中,我们吸收了BAS-WPT中参数标准化的想法,加入了BSAS-WPT算法,来解决步长调参的问题,并取得了一定的改进效果。
2.3 BAS-WPT
相比于2.1.1节中描绘的BAS,
Beetle Antennae Search without Parameter Tuning (BAS-WPT) for Multi-objective Optimization一文给出了改进后的BAS是如何处理步长调节和约束问题抽象的。
2.3.1 与BAS不同之处
BAS-WPT的小尾巴without parameter tunning已经说明了两者之间的区别,即BAS-WPT是不需要进行参数调节的。当然,按照我现在的理解,是BAS-WPT一方面简化了每回合搜索距离(质心到须的距离)的更新,不需要再额外设定与调节诸如\(d_0\),\(\eta_d\)等参数,用户只需要按照式(2.6)来设置\(c_2\)便可;另一方面,参数标准化,让存在量级差异的参数之间不必再像BAS一样,共享一个你不知道该怎么设定的步长\(\delta^t\)(步长过大,小的参数可能经常处于在边界的状态;步长过小,大的参数可能搜索范围达不到)。
那么上述两方面的优势归纳起来是什么呢,那就是你可以设置一个在 \(1\) 附近 \(\delta\) ,然后设定一个衰减率 \(\eta_{\delta}\),以及步长与搜索距离之比 \(c_2\),那么你的天牛就不会出太大的岔子,并且方便调整调节。也就是说,WPT不是让你不用调参,而是减轻了调参的负担。
“不必就纠结归一化处理,之所以这么处理,仅仅是为了调参方便”
— 姜向远
果然,偷懒催生了这一技巧的诞生。不过,我还得再次啰嗦一句标准化的好(是不是我没有接触这个领域,所以喜欢大惊小怪……)。我们在之后,压力容器约束问题(混合整型规划)中,可以看到,待优化参数存在量级差异时,标准化技巧下的步长会比原始的BAS步长设定要更加合理。
2.3.2 约束问题抽象形式
此外,BAS-WPT还为BAS引入了约束问题处理的手段。不过,这和我做模型预测控制时候看到的抽象方式是相同的。我觉得BAS的用户们应该都早已了解,此处就照本宣科。
2.3.2.1 约束问题一般形式
\[\begin{equation} \begin{split} & \frac{\text{Minimize}}{\text{Maximize}} f(\mathbf{x}) \\ s.t. & g_j(\mathbf{x})\leq 0, j=1, \cdots, K \\ & x^\text{max}_i \leq x_i \leq x^\text{min}_i, i=1, \cdots N \end{split} \tag{2.7} \end{equation}\]
\(g_j(\mathbf{x})\leq 0\) 和 \(x^\text{max}_i \leq x_i \leq x^\text{min}_i\) 表示了参数本身的范围和更为精细具体的不等式约束控制。在rBAS包中,我们会有很直观和简便的方式,来设置这些约束。
2.3.2.2 惩罚函数
\[\begin{equation} F(\mathbf{x})=f(\mathbf{x})+\lambda\sum_{j=1}^{K}h_j(\mathbf{x})g_j(\mathbf{x}) \tag{2.8} \end{equation}\]
\[\begin{equation} h_j(\mathbf{x}) = \begin{cases} 1, & g_j(\mathbf{x})>0 \\ 0, & g_j(\mathbf{x})\leq0 \end{cases} \tag{2.9} \end{equation}\]
其中,式(2.8)中的\(\lambda\)表示约束违背的惩罚因子,选取尽量大的正数。而后的\(h_j(\mathbf{x})\)为Heaviside函数,即不等式约束满足时,该函数为0,反之为1。
2.3.3 不足与改进
- 约束处理能力不足
- 缺点:在约束边界上优化目标突变问题的处理上表现不佳
- 改进:二阶
BAS
此处的不足,还需要考虑步长反馈和群体搜索的问题。不过,既然BSAS把姜博的WPT给窃来了,摇身变为了BSAS-WPT,那就不说上述两个问题了。等他日有闲,再去整合李晓晓同学的二阶BAS。
2.4 BAS with momentum(second-order BAS)
带动量的BAS,唔……这名字听着有点长。顾名思义,是利用了惯性项(即,前一时刻的状态),来使得算法不陷入局部最优。不得不说,李晓晓同学对算法的改进既保留了BAS本身的简洁,又增大了BAS对局部最优处理的能力。
在打算复现BSO(BAS和PSO的诚意结合)算法之前,我就看过了李晓晓同学提供给我的二阶BAS代码。相比于BSO,进行了大量的细节上的BAS和PSO融合,二阶BAS只对天牛位置更新的等式(即式(2.3))做了大的改动。因此,我觉得这还是更为类似BAS的,大家接受起来应该也更为容易。
2.4.1 算法原理
在2.1.1节的基础上,改动了一大一小两处地方。大的是,天牛位置更新。小的改动是,步长增加了一个最小分辨率,也就是存在了最小值,不会无限制地缩减。
\[\begin{equation} \mathbf{v}^{t+1} = w_0\mathbf{v}^t - w_1\overrightarrow{b}(f(\mathbf{x}_l^t)-f(\mathbf{x}_r^t)) \tag{2.10} \end{equation}\]
\[\begin{equation} \mathbf{v}^{t+1} = \begin{cases} V_{max},&\mathbf{v}^{t+1} > V_{max} \\ \mathbf{v}^{t+1}, &\mathbf{v}^{t+1} \in [V_{max},V_{max}] \\ -V_{max},&\mathbf{v}^{t+1} <- V_{max} \end{cases} \tag{2.11} \end{equation}\]
\[\begin{equation} \mathbf{x}^{t+1} = \mathbf{x}^t+\mathbf{v}^{t+1} \tag{2.12} \end{equation}\]
大的改动;在式(2.10)中,\(v\)表示速度,\(w_0\)和\(w_1\)分别为常数,也可以理解为权重。前者是上一时刻速度的权重,后者是由左右须函数强度差(类似于梯度)的权重。式(2.11)是对速度范围进行的限定。把式(2.12) 和式(2.3) 相比,不仅多了速度项,还把原有的步长从式中去掉了。
那步长在哪里用呢,有两个地方。
- 用来更新感知距离,也就是质心到须的距离。\(d = \delta/c\),\(c\)是两者之比。
- 用来确定式(2.11)中最大速度\(V_{max}\),即\(V_{max} = c_0 \delta\)。原文中的\(c_0\)和\(w_0\)是用的同一符号,但是在后续的测试函数调试中,两者分开似乎效果更好。因此,在
rBAS中的BASoptim2中,为了更加灵活而将两者区分开来,把选择权给了大家。
此外,还有一个小改动。步长的更新采用了一个最小分辨率,参考式(2.13)。
\[\begin{equation} \delta^{t+1}=\eta_{\delta}(\delta^{t}-\delta_0) + \delta_0 \tag{2.13} \end{equation}\]
如果有必要的话,大家在使用过程中可以设定较小的\(\delta_0\)来规避此项规则。
2.4.2 不足与改进
总的来说,我觉得是大家看完原理,应该就能自己敲出代码的算法。这也反映了该算法的简洁,这和BAS原本的风格应该是一致的。
当然,简洁也意味着可以提升的余地还存在。既然二阶BAS把最精华的惯性项奉上了,我们可以开始对其的改造。此处就不一一罗列。可以参考前面的章节。
就我而言,我觉得BSAS的思路完全可以用在二阶BAS上。这也是由于在某些测试函数上,BSAS更容易地(特指调参简单)达到更优精度给我带来的启发。看来,群体和反馈是一直可以借鉴的思路。
References
Zhang Yinyan, Xu Bin, Li Shuai. 2019. “BAS: Convergence Analysis of Beetle Antennae Search Algorithm and Its Applications.” arXiv. 128.84.21.199/abs/1904.02397.