第 10 章 调参
本章节将会收录一些调参技巧和BAS算法改进的想法。如果大家有好的想法或者研究,欢迎在issues上提出。
10.1 技巧1:高维问题的初始步长设定
李老师指出在高维问题下,BAS及其改进算法由于步长的分量过小,天牛无法有效移动,导致性能不佳。如果该假设成立,则在处理类似问题时在初始化步长时,在原有的参数选择上,乘以 \(\sqrt{n}\),其中\(n\)是待优化变量的维度。
10.1.1 原理
在章节2.1.1的式(2.1)中,我们给出了BAS生成随机方向并标注化的式子,如下所示。
\[ \overrightarrow{\mathbf{b}}=\frac{\text{rnd}(n,1)}{\|\text{rnd}(n,1)\|} \] 此后,利用上述的方向和两须的函数差值来计算下次天牛的位置,如式(2.3).方便起见,同样在此处给出。
\[ \mathbf{x}^t=\mathbf{x}^{t-1}+\delta^t\overrightarrow{\mathbf{b}}\text{sign}(f(\mathbf{x}_r)-f(\mathbf{x}_l)) \tag{2} \]
方向向量 \(b\) 会与 步长 \(\delta^t\) 直接相乘,直接影响下一次的天牛位置。高维度问题,\(b\) 的每个元素在标准化后都较小。这也会使得步长\(\delta^t\)在每个方向的分量都很小。即,天牛只能在这个方向上走动一段很小的距离。这个现象会随着问题维度的增加而变得严重。
此前,有同学反映,即使是对于简单的 \(f = \sum x_i^2\) 问题,在维度高了之后,BAS算法的效果也会变差。这个例子将用于本文来验证这个现象,以及上述的改进策略是否有效。
10.1.2 测试函数
测试函数如式
\[\begin{equation} f = \sum_{i=1}^{n}x_i^2 \tag{10.1} \end{equation}\]
10.1.3 BAS测试代码
代码用R语言编写,直接调用rBAS包,大家也可以用matlab来实现,因为在BAS上只要改变初始步长即可以重复此处实验。
在R语言中给定目标函数。
两种策略的比较,一种是原始的BAS,一种是初始步长乘以维度。 实验取的向量长度分别为2,4,6…40。
test_BAS <- function(dims){
m <- dims
fit_sqrt <- BASoptim(fn = obj,
init = rep(5,m),
lower = rep(-10,m),
upper = rep(10,m),
trace = F,
d1 = 1,
step = (1*sqrt(m)),eta_d = 0.98,n = 200,
steptol = .Machine$double.eps,seed = 1)
fit_raw <- BASoptim(fn = obj,
init = rep(5,m),
lower = rep(-10,m),
upper = rep(10,m),
trace = F,
d1 = 1,
step = 1,eta_d = 0.98,n = 200,
steptol = .Machine$double.eps,seed = 1)
result <- c(BAS_modified = fit_sqrt$value,
BAS_original = fit_raw$value)
return(result)
}
dimsx <- seq(2,40,by = 2)
dims <- matrix(data = dimsx, nrow = 1)
BAS_experiment <- apply(dims,2,test_BAS)10.1.4 BAS测试结果
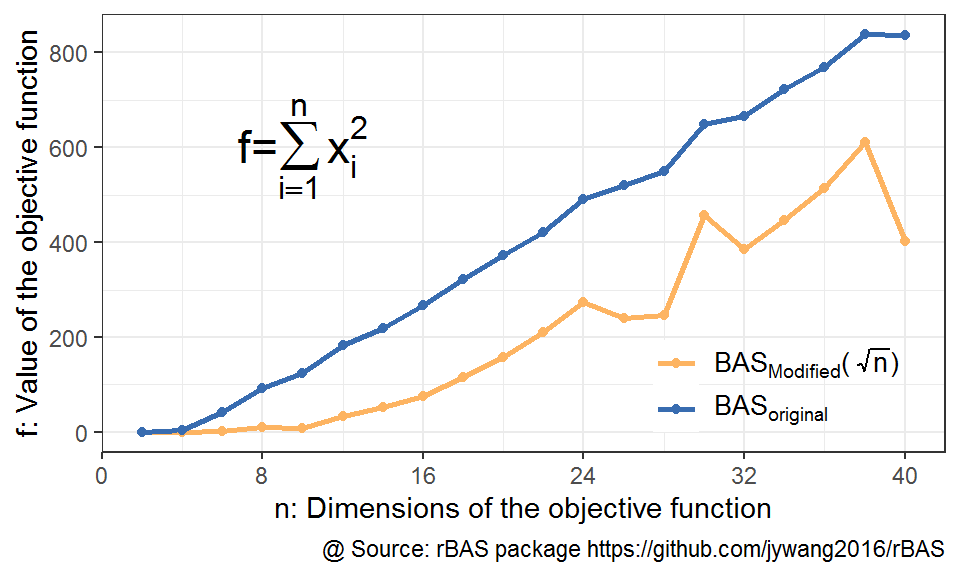
图 10.1: 高维优化问题下BAS不同初始步长结果对比
从结果可以看到,橙色线代表的改进策略,会带来显著的效果提升。
10.1.5 BSAS 测试代码
同样,对BSAS算法的不同粒子数量的取值,也分别进行了对比实验。同样,维度也是从2到40。
test_BSAS <- function(dims,k){
m <- dims
fit_sqrt <- BSASoptim(fn = obj,
init = rep(5,m),
lower = rep(-10,m),
upper = rep(10,m),
trace = F,
k = k,
step = 1*sqrt(m),
d1 = 1,eta_d = 0.98,n = 200,
steptol = .Machine$double.eps,seed = 1)
fit_raw <- BSASoptim(fn = obj,
init = rep(5,m),
lower = rep(-10,m),
upper = rep(10,m),
trace = F,
k = k,
step = 1,
d1 = 1,eta_d = 0.98,n = 200,
steptol = .Machine$double.eps,seed = 1)
result <- c(BSAS_modified = fit_sqrt$value,
BSAS_original = fit_raw$value)
return(result)
}
BSAS_experiment <- apply(dims,2,test_BSAS,k=1)10.1.6 BSAS测试结果
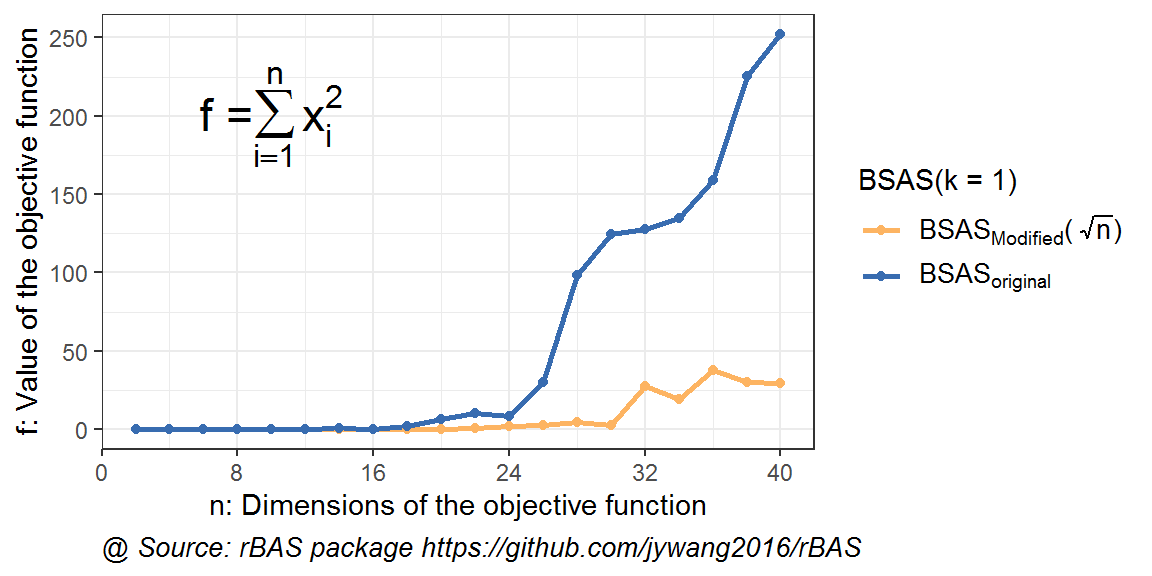
图 10.2: 高维优化问题下BSAS不同初始步长结果对比
对于只有一个粒子的BSAS算法(即只在步长自适应上进行优化的BAS),在维度升高的时候,改进策略也是成功的。当然,总体而言,两种情况均比BAS对应的情况效果要优。
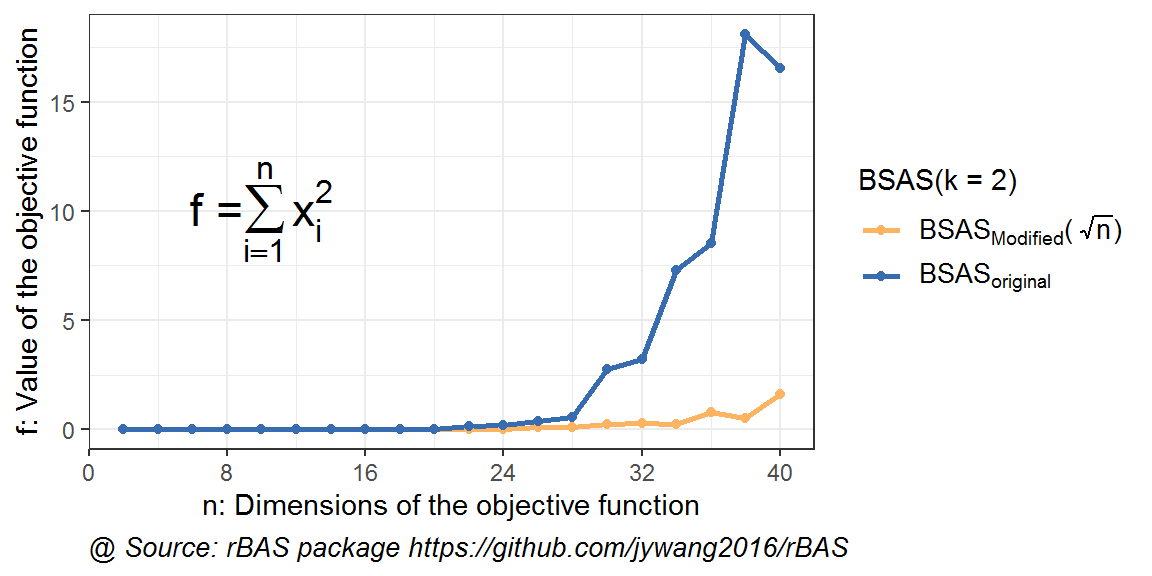
图 10.3: 高维优化问题下BSAS(k=2)不同初始步长结果对比
在上图中可以看到,在粒子数增加到2之后,算法的结果也证实了策略的可用。但是,两种方法结果接近的维度会更加延后。在30维度的时候,才开始出现了显著差异。一方面表明粒子数对算法的提升,另一方面,也说明了这个策略在越高维度的时候,效果也愈加显著。
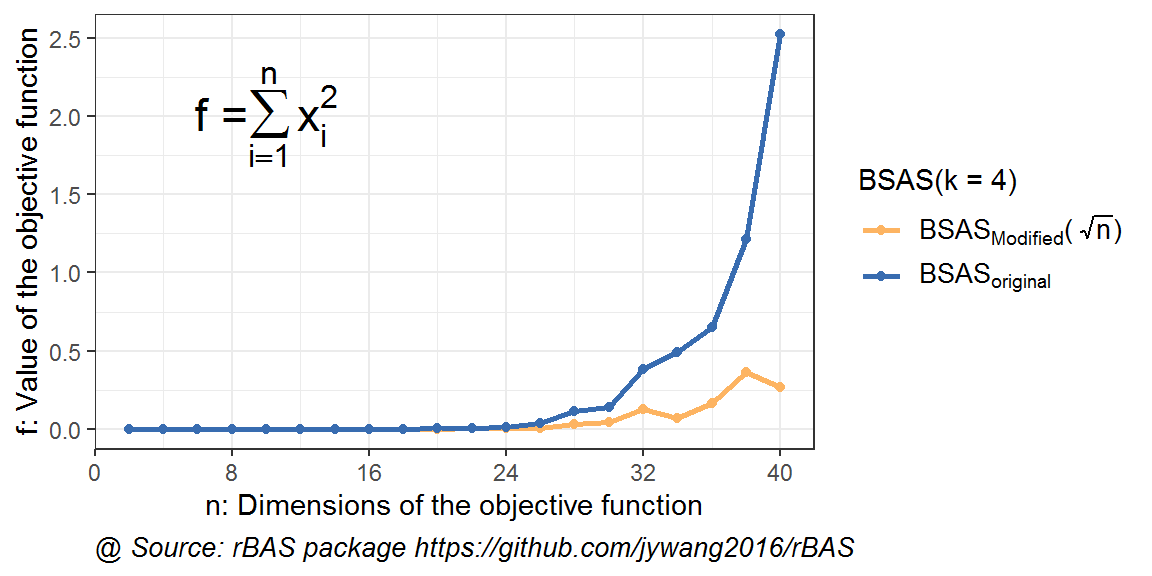
图 10.4: 高维优化问题下BSAS(k=4)不同初始步长结果对比
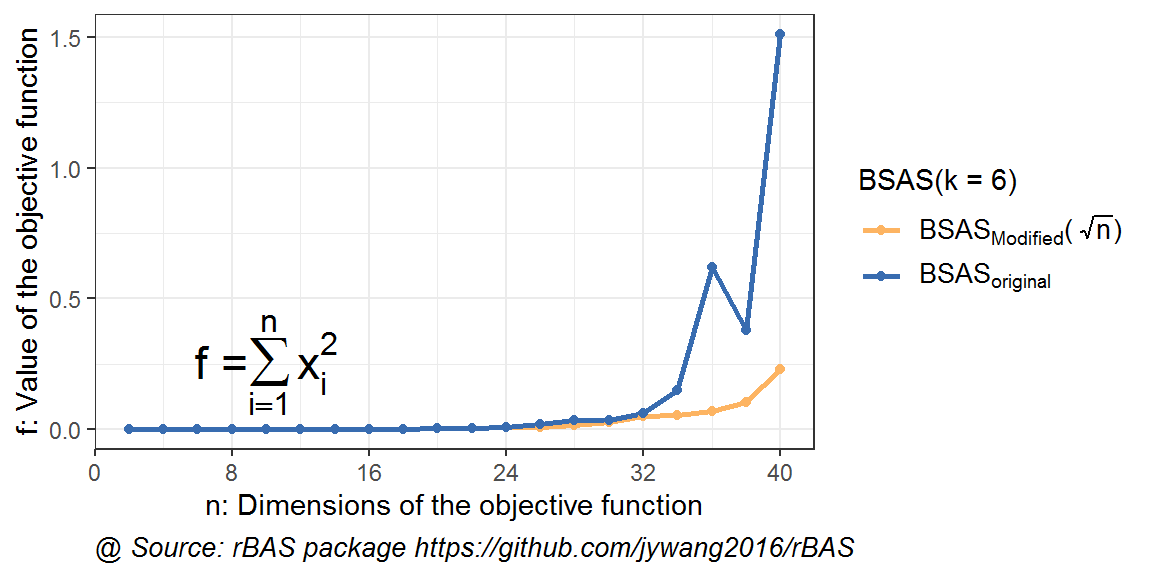
图 10.5: 高维优化问题下BSAS(k=5)不同初始步长结果对比
同样,可以看到在粒子数增加时,BSAS算法的效果也在逐渐优化。而加入了改进初始步长策略,橙线对应的结果也要优于蓝色线条的。总体来说,该算法在BAS和BSAS的情况下都是凑效。
10.1.7 总结
从上述测试的结果可以看到,在优化问题维度提高时,按照原有经验选择的初始步长,可能会导致算法效果不佳。
当然,大家可以还是按照原来的经验,即根据参数范围来估计一个初始步长。只要记得最后在高维问题时乘以对应的 \(\sqrt{n}\)即可。这样算法在高维下会体现出更优的性能。
10.2 技巧2: 步长衰减率设定
为了解决高维度问题,李帅老师提出了两个改进策略。第一个,即为此前文档中描述的将初始步长乘以\(\sqrt{n}\)改进步长分量过小的问题。第二个,即本文档中讨论的是,步长衰减率设定为\(\eta = \eta_0^{\frac{1}{n}}\)。
- 改进策略1(BAS_tricks1): 初始步长乘以\(\sqrt{dims}\)。在维度提高后,步长相应提高,在每个维度上的分量也会相应提高,不至于让天牛在中后期走不动。
- 改进策略2(BAS_tricks2):步长衰减率设定为\(\eta = \eta_0^{\frac{1}{n}}\),其中,\(\eta_0\)可设定为0.98。每次迭代,保证了n维搜索空间体积缩减为原来的\(\frac{1}{\eta_0}\)。
10.2.1 代码
测试函数如(10.1)。
代码用R语言编写,直接调用
rBAS包,大家也可以用matlab来实现,因为在BAS上只要改变初始步长step与衰减比例eta_step即可重复此处实验。
library(patchwork)
obj <- function(x){
return(sum(x^2))
}
test_BAS <- function(dims,c_init,n){
m <- dims
fit_raw <- BASoptim(fn = obj,
init = rep(5,m),
lower = rep(-10,m),
upper = rep(10,m),
trace = F,
d1 = 1,eta_d = c_init,
step = 1,eta_step = c_init,n = n,
steptol = .Machine$double.eps,seed = 1)
fit_tricks2 <- BASoptim(fn = obj,
init = rep(5,m),
lower = rep(-10,m),
upper = rep(10,m),
trace = F,
d1 = 1,eta_d = c_init^(1/m),
step = 1,eta_step = c_init^(1/m),n = n,
steptol = .Machine$double.eps,seed = 1)
fit_tricks1 <- BASoptim(fn = obj,
init = rep(5,m),
lower = rep(-10,m),
upper = rep(10,m),
trace = F,
d1 = 1,eta_d = c_init,
step = 1*sqrt(m),eta_step = c_init,n = n,
steptol = .Machine$double.eps,seed = 1)
result <- c(BAS_original = fit_raw$value,
BAS_tricks1 = fit_tricks1$value,
BAS_tricks2 = fit_tricks2$value)
return(result)
}
dimsx = seq(2,40,by = 2)#维度设定为2,4,6...40
dims <- matrix(data = dimsx, nrow = 1)
BAS_experiment <- apply(dims,2,test_BAS,c_init = 0.98,n = 200)结果如下图所示。
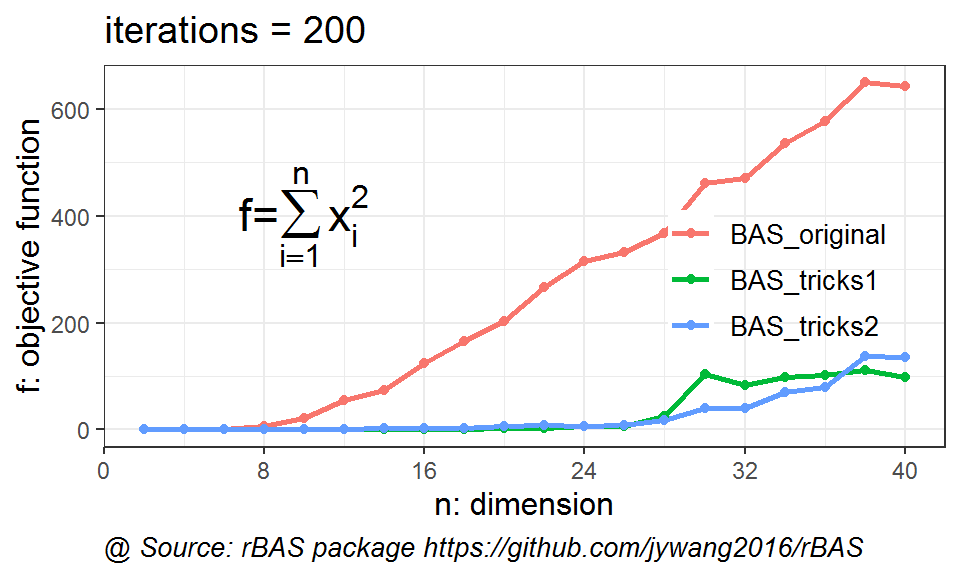
图 10.6: 不同维度虾两种改进BAS与原始BAS算法性能对比
从上图来看,2种策略都能够有效地防止天牛提前老化。
此外,还可以进一步探索,迭代次数的不同,结果的变化。
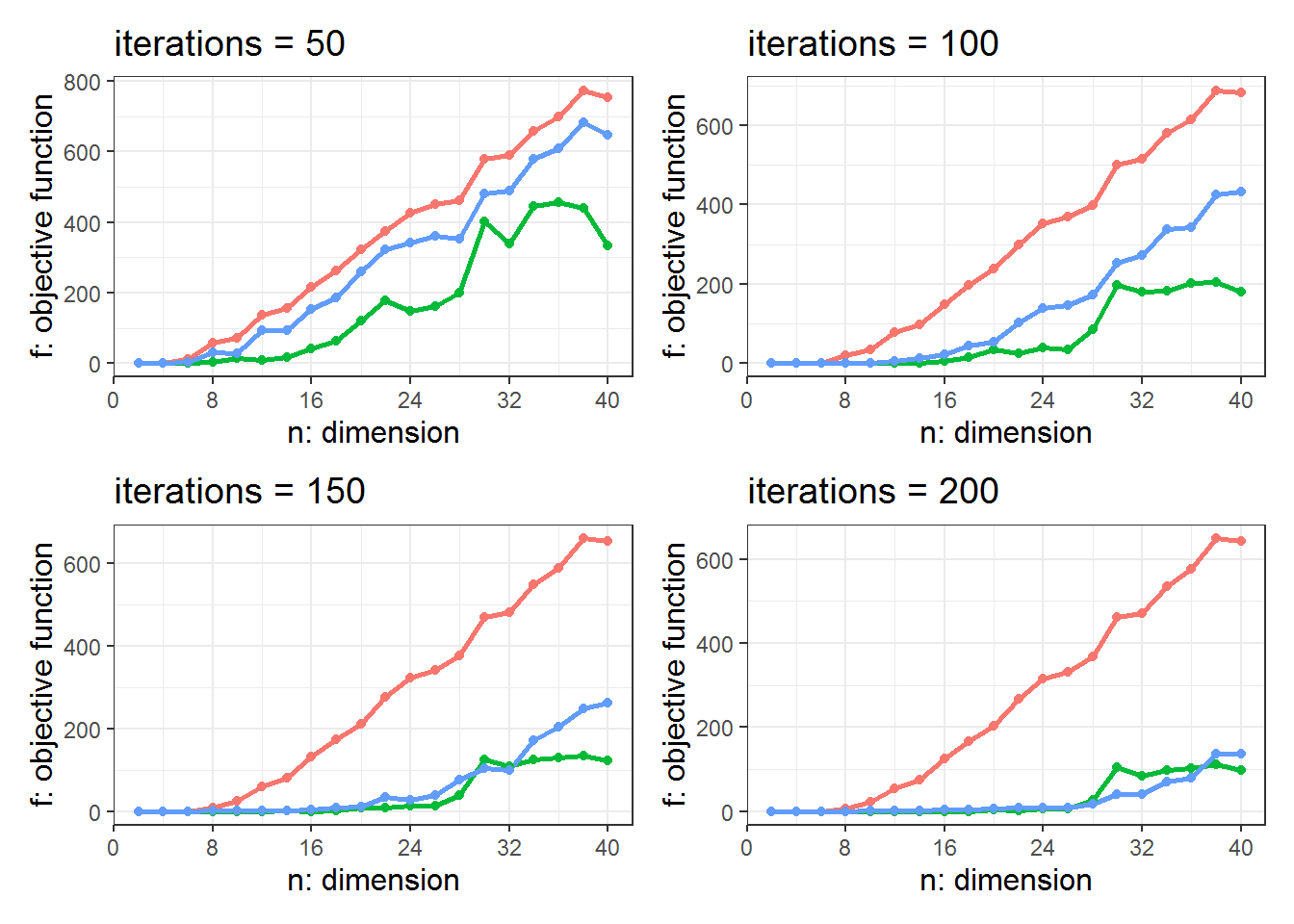
图 10.7: 不同迭代次数下,两种改进BAS与BAS算法的性能对比
原始的BAS,由于步长衰减过快,在迭代次数从50至200的变化中,没有得到效果的提升。而改进的BAS算法,则会随着迭代次数的提升,获得效果上的提升。
tricks2的步长设置,保证了搜索空间每次缩小\(1/\eta_0\)。相较于步长衰减设定为\(\eta_0\)时,搜索空间每次缩小\(1/\eta_0^{dims}\)而言,tricks2的技巧让天牛不至于迅速老化,由于步长过小而“走不动”。
10.3 技巧3:按照维度设定步长初始值和衰减率
是否有可能融合两种tricks的优点呢?假设存在技巧3,考虑\(\eta = \eta_0^{\frac{1}{1+p}}=\eta_0^{\frac{1}{1+k_0(n-1)}}\),其中,\(k_0\in [0,1]\),\(\eta_0\)为常用的步长衰减系数,如0.98。而步长的初始值设定为\(step = step_0 * \sqrt{dims}\),其中,\(step_0\)是步长的初始值,\(dims\)是问题的维度。
可以看到,当\(k_0=0\)的时候,技巧3就退化为了技巧1,当\(k_0=1\)的时候,技巧3就变为了步长乘以了维度平方根的技巧2。我们可以利用一些仿真实验,来看在\(k_0\)取值对优化结果的影响,以及是否会获得较技巧2和3更好的效果。
test_BAS <- function(dims,c_init,n,k0){
m <- dims
c_power <- k0 * (m - 1)
fit_raw <- BASoptim(fn = obj,
init = rep(5,m),
lower = rep(-10,m),
upper = rep(10,m),
trace = F,
d1 = 1,eta_d = c_init,
step = 1,eta_step = c_init,n = n,
steptol = .Machine$double.eps,seed = 1)
fit_tricks1 <- BASoptim(fn = obj,
init = rep(5,m),
lower = rep(-10,m),
upper = rep(10,m),
trace = F,
d1 = 1,eta_d = c_init,
step = 1*sqrt(m),eta_step = c_init,n = n,
steptol = .Machine$double.eps,seed = 1)
fit_tricks2 <- BASoptim(fn = obj,
init = rep(5,m),
lower = rep(-10,m),
upper = rep(10,m),
trace = F,
d1 = 1,eta_d = c_init^(1/m),
step = 1,eta_step = c_init^(1/m),n = n,
steptol = .Machine$double.eps,seed = 1)
fit_tricks3 <- BASoptim(fn = obj,
init = rep(5,m),
lower = rep(-10,m),
upper = rep(10,m),
trace = F,
d1 = 1,eta_d = c_init^(1/(1+c_power)),
step = 1*sqrt(m),eta_step =c_init^(1/(1+c_power)),n = n,
steptol = .Machine$double.eps,seed = 1)
result <- c(BAS_original = fit_raw$value,
BAS_tricks1 = fit_tricks1$value,
BAS_tricks2 = fit_tricks2$value,
BAS_tricks3 = fit_tricks3$value)
return(result)
}dimsx <- seq(2,40,by = 2)
dims <- matrix(data = dimsx, nrow = 1)
BAS_experiment <- apply(dims,2,test_BAS,c_init = 0.95,n = 200,k0 = 0)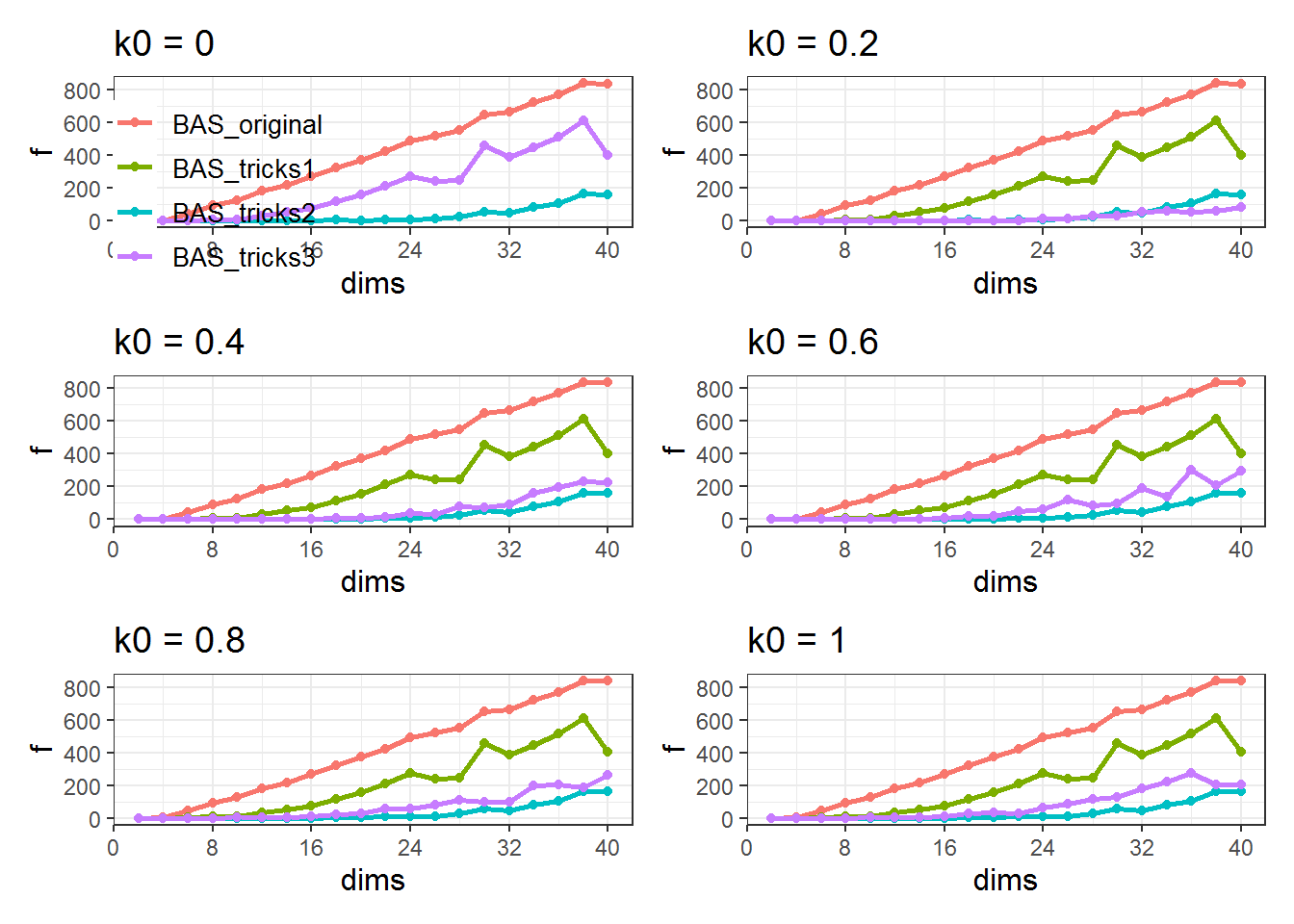
图 10.8: 不同k0值三种改进BAS与原始BAS算法性能对比
可以看到,在\(k_0 = 0\)的时候,技巧3的曲线与技巧1重合.而在\(k_0 = 0.2\)时,技巧3的效果表现得最好,优于技巧1和2。随着\(k_0\)继续增大,技巧3的结果曲线变化,在技巧2对应的结果曲线附近发生波动。可以猜测,\(k_0 = 0.2\)左右处,技巧3在当前参数配置下的寻优效果最佳。
大家可以在调参时,按照上面的技巧来设定步长初始值及衰减率。更好的方法是,按照技巧3的设定,将调步长与衰减率转为调节变量\(k_0\)。
10.4 判断迭代终止时算法收敛状况
李老师指出目前可能存在三种比较常见的迭代终止原因。
- 算法陷入局部极值
- 步长太小,天牛走不动,但是并未达到局部极值
- 天牛走得动,并非局部极值,但是迭代次数已到,终止了迭代
对结果进行相应的判断,并做出对策,有利于做出进一步地参数优化,甚至是算法改进。
如,如果属于情况1,可以尝试在原来的优化基础上,重新给定大的步长,帮助算法跳出当前的局部极值,达到更优的局部极值;情况2,也可以通过给定合适的步长大小来改善;情况3,可以考虑增加迭代次数。
同样地,我们采用两个测试函数来解释上述的情况,并验证对应方案的效果。
10.4.1 实验1
实验1利用简单的测试函数,来对比BAS和BSAS在高维问题下的结果,以及出现问题的原因(属于三种情况的哪一种),来给出改进或者调试的思路。
测试函数如式(10.1)所示。该函数在\(x_i = 0\)处取得全局最优。
10.4.1.1 BAS算法
利用BAS搜索目标函数的最优值,设置迭代次数为200,维度为10。
rm(list = ls())
library(rBAS)
library(numDeriv)
obj <- function(x){
return(sum(x^2))
}
BASn <- function(n,dims,init = rep(5,m)){
m <- dims
fit_BAS <- BASoptim(fn = obj,
init = init,
lower = rep(-10,m),
upper = rep(10,m),
trace = F,
d1 = 1,
step = (1*sqrt(m)),eta_d = 0.98,n = n,
steptol = .Machine$double.eps,seed = 1)
return(fit_BAS)
}## [1] 1.25580526 0.23166118 0.71917160 -0.42806595 1.12091543
## [6] 1.62701181 1.18880886 0.58474173 0.09426773 0.62736667## [1] 8.392446可以看到,在200次迭代之后,天牛所处的位置并没有接近最优值,即 \(x = 0\),其中的部分元素接近于0。最后的函数值是8.4。
此时的步长如下:
## NULL为1e-4,这表明此时的步长偏小,天牛所处的位置与最优点的距离为步长量级的\(10^4\)倍。因此,本实验属于上述的情况2,步长太小,走不动。
此种情况可以通过在上回合的优化结果下,重新给定合适的大步长来得到更优的结果。
## [1] 0.034425449 0.011889588 0.021235726 0.017903444 0.041177485
## [6] -0.023956800 0.008979989 0.005722928 0.024887352 -0.001700370## [1] 0.00510314可以看到,此时的函数值已经十分接近于最优值,方法凑效。
此时的步长如下:
## NULL由于步长和优化的坐标之间仍然存在量级的差距,还是表明在这个位置,哪怕每次都是朝着最优位置走,天牛也迈不开步子,我们可以再次使用重新给定步长的手段。
## [1] -0.0011431003 -0.0031872963 -0.0039303321 0.0020186072 0.0021288149
## [6] 0.0001232545 -0.0019088662 -0.0037557675 0.0003802965 -0.0010499301## [1] 5.45314e-05可以看到,优化结果更加接近于最优值。
此时的步长如下:
## NULL为了方便起见,同时列出三次寻优的结果
## [1] 8.392446## [1] 0.00510314## [1] 5.45314e-05结果不断地接近最优值。这表明在上述情况2出现时,在现有的结果上,重新给定大的步长,然后再次寻优是凑效的。也就是,需要重新让天牛能走起来。当然,方法本身也不可能每次都凑效,此时需要大家在调试成本和结果优化之间寻求一个平衡。
10.4.1.2 BSAS算法
BAS问题的关键在于步长的衰减没有反馈机制,不管结果好坏,步长都会衰减。尝试使用BSAS算法进行寻优,结果如下:
BSASn <- function(n,dims,k){
m <- dims
fit_BSAS <- BSASoptim(fn = obj,
init = rep(5,m),
lower = rep(-10,m),
upper = rep(10,m),
trace = F,
k = k,
step = 1*sqrt(m),
d1 = 1,eta_d = 0.98,n = n,
steptol = .Machine$double.eps,seed = 1)
return(fit_BSAS)
}
fit_BSAS1 <- BSASn(n = 200, dims = 10,k = 1)
fit_BSAS1$par;fit_BSAS1$value;fit_BSAS1$step## [1] -0.0004297315 -0.0093523824 0.0077216584 0.0016681671 0.0032866863
## [6] -0.0128492187 0.0085156508 -0.0104277522 -0.0030415481 0.0228343806## [1] 0.001037878## NULL可以看到BSAS算法的结果是 0.001,比BAS算法进行了一次重新设定步长后的结果更优。猜测是因为步长反馈调节策略使得步长衰减得更合理所致。
由于此时的步长是0.019,稍大于天牛所在位置的元素。因此,认为属于情况3,即由于迭代次数不够,导致没能到达最优(局部最优)位置。所以,加大迭代次数来看效果。
## [1] -1.610736e-06 2.899101e-07 -4.068405e-08 -2.802695e-07 -1.098365e-06
## [6] -6.222215e-08 8.150385e-07 -7.817550e-07 -1.019755e-06 1.515487e-06## [1] 8.581032e-12## NULL可以看到,在迭代次数为500时,结果更优,为\(8.58*10^{-12}\)。而步长\(2.14*10^-6\)仍然是和位置的元素量级保持一致。因此,推测可以继续加大迭代次数来获得更优的结果。
## [1] -3.785371e-13 -1.806485e-13 2.075196e-13 -3.060651e-13 3.156182e-14
## [6] -6.596821e-14 1.428151e-13 -1.098809e-13 9.320642e-14 -1.186302e-13## [1] 3.732429e-25## NULL可以看到,随着迭代次数的提升,结果不断优化。当前条件下的目标函数值为\(3.73*10^{-25}\)。
方便起见,列出三次实验结果。
## [1] 0.001037878## [1] 8.581032e-12## [1] 3.732429e-2510.4.1.3 总结
对于测试函数 \(f = \sum x_i^2\),
- BAS出现情况2,即步长太小,导致天牛走不动。这是由于BAS的步长衰减策略造成的。保持上一次的优化结果(作为下次优化的初始值),重新设定大的步长可以解决此类问题。
- BSAS出现情况3,即步长是能让天牛走动的,但迭代次数终止了算法。这是因为BSAS的步长是根据结果反馈来调节的,不至于衰减得太小导致天牛走不动。对于此类情况,延迟迭代次数的调差方法可以提高结果。
一般的情况是,如果算法求得的位置,其中的元素大小远超步长大小,那么应该是属于情况2,要考虑重新设定步长。如果元素大小和步长大小量级相仿,则可以考虑增加迭代步长。
10.4.2 实验2
实验2 利用存在较多局部最优的函数,来对比BAS和BSAS的结果,试图找出问题出现的原因,以及对应的改进思路。
10.4.2.1 测试函数
\[\begin{equation} f=10*m - \sum_i^m (x_i^2-10*cos(2\pi x_i)) \quad x_i\in[-5.12,5.12] \tag{10.2} \end{equation}\]
测试函数在 \(x_i = 0\) 处取得最优值 \(f = 0\) 。
图10.9为测试函数2维时的取值分布。从中可以看到,等值线在接近 \(x = (0,0)\)时颜色加深,表明接近最小值。
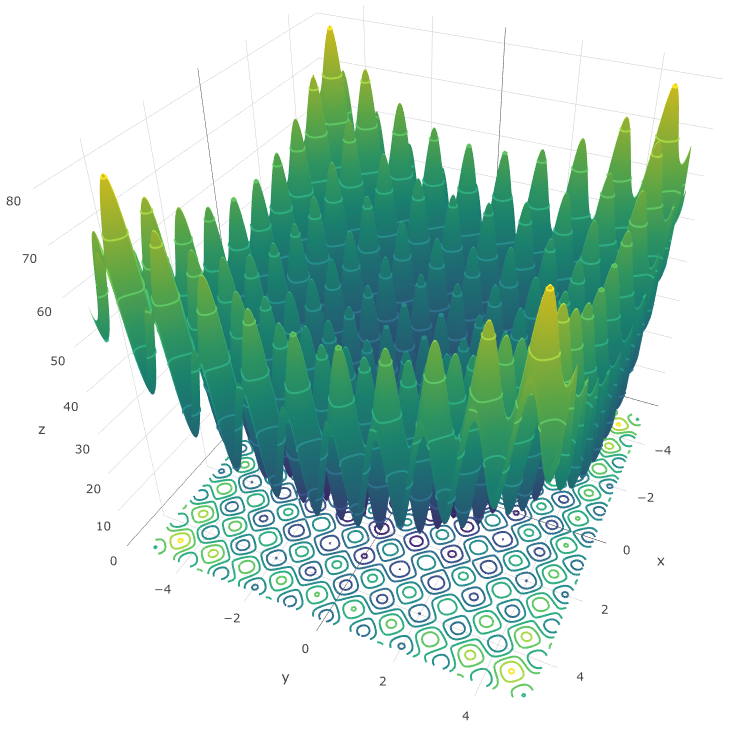
图 10.9: Fig.1 Rastrigin function
10.4.2.2 BAS算法
BAS_Rast_n <- function(n,dims,init = rep(5,dims),seed = 1){
m <- dims
fit_BAS <- BASoptim(fn = Rast,
init = init,
lower = rep(-5.12,m),
upper = rep(5.12,m),
trace = F,
d1 = 1,
step = (1*sqrt(m)),eta_d = 0.98,n = n,
steptol = .Machine$double.eps,seed = seed)
return(fit_BAS)
}
fit_Rast <- BAS_Rast_n(n = 200, dims = 5)
fit_Rast$par; fit_Rast$value## [1] -1.869276e-05 -9.950173e-01 1.989897e+00 4.974418e+00 1.989810e+00## [1] 33.82836结果与\((0,0,0,0,0)\)还是存在较大的差距。
## NULL此时的步长为 \(7.8*10^{-5}\),天牛也存在走不动的现象。此处的梯度为
## [1] -0.007423366 -0.023255606 -0.006154134 -0.106994981 -0.040438609从梯度接近于0来看,应该是陷入了局部最小值,也就是属于情况1。我们再给定一个大的步长,重新搜索。
fit_Rast <- BAS_Rast_n(n = 200, dims = 5,
init = fit_Rast$par,seed = 1)
fit_Rast$par; fit_Rast$value;fit_Rast$step## [1] -1.9898668 -0.9949566 -0.9950607 1.9898565 0.9949586## [1] 10.94454## NULL可以得知,结果进一步提升。此时的梯度是
## [1] 0.0180051671 0.0007939765 -0.0404656270 -0.0220834035 -0.0000156832同样,梯度十分接近于0,表明此处是一个局部最小值。即对于情况1,重新使用大的步长也能改善优化结果,有助于找到一个更优的局部最小值。换一个初始步长,可能会导致策略失效,即这样的策略也需要辅以调差。感兴趣的同学可以自行调节代码。
10.4.2.3 BSAS算法
BSAS_Rast_n <- function(n,dims,k = 1,init = rep(5,dims),seed = 1){
m <- dims
fit_BSAS <- BSASoptim(fn = Rast,
init = init,
lower = rep(-5.12,m),
upper = rep(5.12,m),
trace = F,
d1 = (1*sqrt(m)),
k = k,
step = (1*sqrt(m)),eta_d = 0.98,n = n,
steptol = .Machine$double.eps,seed = seed)
return(fit_BSAS)
}
fit_Rast <- BSAS_Rast_n(n = 200,k = 1, dims = 5,seed = 1) #2,2
fit_Rast$par; fit_Rast$value;fit_Rast$step## [1] 2.984883 3.979838 1.989614 4.974257 2.984340## [1] 62.68211## NULL梯度如下
## [1] 0.01066209 0.02145915 -0.11811262 -0.17008744 -0.20354255结果比BAS要差,且从梯度来看,算法已经达到了局部极值,属于情况1。
此时沿用实验1中的结论,打算重新使用大的步长使其跳出局部极值。
m = 5
n = 200
k = 1
seed =1
fit_Rast <- BSASoptim(fn = Rast,
init = fit_Rast$par,
lower = rep(-5.12,m),
upper = rep(5.12,m),
trace = F,
d1 = (1*sqrt(m)),
k = k,
#p_step = 0.8,
step = 3,eta_d = 0.98,n = n,
steptol = .Machine$double.eps,seed = seed)
fit_Rast$par; fit_Rast$value;fit_Rast$step## [1] 2.984560 3.979510 1.989868 4.974568 2.984608## [1] 62.68205## NULL从结果看来,并未有改善。
## [1] -0.11667250 -0.10781782 -0.01768515 -0.04851506 -0.09778878从梯度看,算法仍然处于陷入了局部最优
10.4.2.4 BSAS步长更新概率
还是考虑从步长着手,设置\(p_{step}\)参数为0.8,即有0.8的概率,哪怕找不到更优的位置,天牛也有0.8的概率会保持当前的步长继续搜索。尽管BSAS是根据结果反馈来调节步长的,在局部极值过多的情况下,找不到更优值,也会使得BSAS的步长一直衰减。
可以会有同学担心,如果\(p_{step}\)过大,又找不到更优位置,步长一直不更新怎么办。由于BSAS算法中有\(n_{flag}\)参数来限制步长不更新的次数,因此不会出现找不到更优解一直保持原步长的现象。
n = 400
fit_Rast <- BSASoptim(fn = Rast,
init = fit_Rast$par,
lower = rep(-5.12,m),
upper = rep(5.12,m),
trace = F,
d1 = (1*sqrt(m)),
k = k,
p_step = 0.8,
step = 3,eta_d = 0.98,n = n,
steptol = .Machine$double.eps,seed = seed)
fit_Rast$par; fit_Rast$value;fit_Rast$step## [1] 9.956177e-01 2.985797e+00 3.578282e-05 1.989544e+00 2.983359e+00## [1] 22.88472## NULL可以看到,结果存在较大的提升。
10.4.2.5 天牛数
此外,由于测试函数的局部极小值过多,尝试在每回合多派天牛出去探索。
k = 12
n = 400
seed =1
fit_Rast <- BSASoptim(fn = Rast,
init = fit_Rast$par,
lower = rep(-5.12,m),
upper = rep(5.12,m),
trace = F,
d1 = (1*sqrt(m)),
k = k,
step = 3,eta_d = 0.98,n = n,
steptol = .Machine$double.eps,seed = seed)
fit_Rast$value;fit_Rast$par## [1] 5.969749## [1] -4.976151e-07 1.989909e+00 -1.273845e-06 9.949561e-01 9.949542e-01## [1] -0.0001974462 -0.0013999122 -0.0005054414 -0.0010068239 -0.0017417871效果也得到了改善,从梯度上看,达到了新的局部最小值。
10.4.2.6 总结
此前提出的改善方法(主要集中在步长的策略),在复杂的测试函数下,仍然适用。
在局部最小值较多的复杂测试函数下,步长不能轻易衰减。BSAS算法在提高了步长不衰减的概率参数后效果出现了提高。而没有设置该参数的情况下,步长很容易衰减到很小(因为BSAS的逻辑是效果不改善就减小步长),导致无法跳出局部最小。
在进入局部最小值后,提高天牛数目和给定大的步长重新寻优策略结合使用,可以使得效果进一步提高。
总的来说,这些技巧都是希望大家能重新审视优化过程中步长的变化策略。大家也可以根据不同的问题,自己指定一些步长的衰减策略。
有意思的是,BSAS在\(k=1\)时,其实就是步长根据结果反馈调节的BAS。也就是,下一步找得到更优的位置,天牛就保持当前步长,继续寻优;反之,则步长衰减。尽管有很多参数限制BSAS不要过于贪婪,但遇到复杂的优化问题时(如实验2),找不到更优位置,BSAS的步长也如同BAS一样,一直衰减。
而对\(p_{step}\)参数的调节,更像是对不同的问题,给出的不同的步长衰减策略。因此,大家不必局限于BSAS算法,完全可以在BAS算法和自己的问题基础上,改进适合自己的步长调节策略。
最后,rBAS的下一次更新,将包含对算法的结果做出判断,并给出可能的参数改进建议的功能。判断依据和改进建议来自于上面的实验。