第 7 章 BAS案例二:龙门起重机运动控制
由群友李晓晓同学提供案例。
7.1 问题背景
龙门起重机(gantry crane),如图7.1所示,是水平桥架设置在两条支腿上构成门架形状的一种桥架型起重机。起重小车trolley在桥架上运行,利用绳索(cable)一类的柔性体连接负载(load)。在负载的输送过程中,load的摆动问题一直是影响吊车装运效率提高的一大难题。
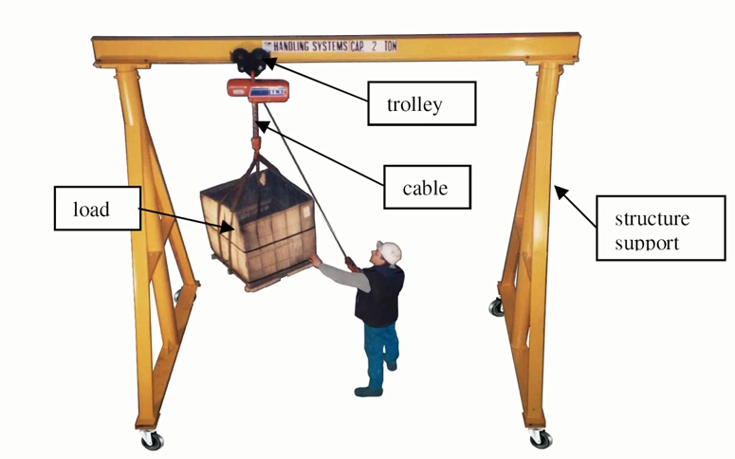
图 7.1: 龙门起重机示意
模型可以简化为图7.2。重物通过绳索与小车相连,小车在外力的作用下水平运动,小车质量为M(kg),重物的质量为m(kg),绳索的长度为r(m),\(\theta\)为摆角,x表示水平方向上的位移。
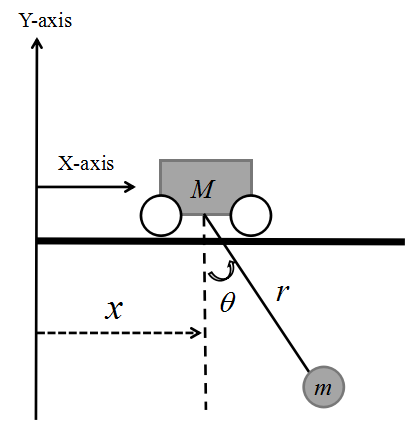
图 7.2: 龙门起重机模型
7.2 优化问题抽象
优化的变量为bang-coast-bang控制中,\(x = [tp_1,tp_2,tf]^T\),两个给予脉冲加速度激励的时段以及全部的作业时间,以此来使得负载的摆角(优化目标)最小。
取小车的位置x,摆角\(\theta\)作为系统的广义坐标系。小车和负载在t时刻的位置坐标如式(7.1)所示。
\[\begin{equation} \begin{cases} x_M(t)&=\quad x(t)\\ y_M(t)&=\quad 0 \\ x_m(t)&=\quad x(t)+rsin\theta(t)\\ t_m(t)&=\quad -rco\theta(t) \end{cases} \tag{7.1} \end{equation}\]
因此,对\(t\)求导,得到小车和负载的速度分量如式(7.2)所示。
\[\begin{equation} \begin{cases} \dot{x}_M(t) &=\quad \dot{x}_t\\ \dot{y}_M(t) &=\quad 0\\ \dot{x}_m(t) &=\quad \dot{x}(t)+r\dot{\theta}(t)cos\theta(t)\\ \dot{y}_m(t) &=\quad r\dot{\theta}(t)sin\theta(t) \end{cases} \tag{7.2} \end{equation}\]
系统动能如式(7.3):
\[\begin{equation} \begin{split} T = &\frac{1}{2}MV_M^2(t) + \frac{1}{2}mV_m^2(t) \\ =&\frac{1}{2}M(\dot{x}_M^2(t)+\dot{y}_M^2(t))+\frac{1}{2}m(\dot{x}_m^2(t)+\dot{y}_m^2(t))\\ =&\frac{1}{2}M\dot{x}_M^2(t) + \frac{1}{2}m\dot{x}_m^2(t) + \\ &\frac{1}{2}mr^2\dot{\theta}^2(t) + mr\dot{x}(t)\dot{\theta}(t)cos\theta(t) \end{split} \tag{7.3} \end{equation}\]
势能如式(7.4):
\[\begin{equation} P = -mgrcos\theta(t) \tag{7.4} \end{equation}\]
通过式(7.4)和式(7.3),我们可以得到拉格朗日方程,即\(L = T -P\)。根据欧拉-拉格朗日方程(Euler-Lagrangian equation),龙门起重机的动力学模型如式(7.5)所示。
\[\begin{equation} \frac{d}{dt}[\frac{\partial{L}}{\partial{\dot{q_k}}}] - \frac{\partial{L}}{\partial{q_k}}=Q_k, \quad k=1,\cdots,n \tag{7.5} \end{equation}\]
其中,\(n\)表示系统的自由度,\(\{q_1,\cdots,q_n\}\)表示广义坐标集合,\(\{Q_1,\cdots,Q_n\}\)表示广义的驱动力(对应于各自的广义坐标)。把摆角作为广义坐标,可以得到式(7.6)。
\[\begin{equation} \frac{d}{dt}[\frac{\partial{L}}{\partial{\dot{\theta}}}] - \frac{\partial{L}}{\partial{\theta}}=0 \tag{7.6} \end{equation}\]
第一项为\(mr^2\ddot{\theta}(t)+mr\ddot{x}(t)cos\theta(t)\),第二项为\(-mgrsin\theta(t)\),代入式(7.6)中可以得到\(\theta\)的求解方程,即式(7.7)。
\[\begin{equation} \ddot{\theta}(t)=-\frac{\ddot{x}(t)cos\theta(t)+gsin\theta(t)}{r} \tag{7.7} \end{equation}\]
通过求解该方程,我们可以得到我们的优化目标。
7.3 优化理论
优化理论为二阶BAS算法。李晓晓同学给出的参数是,\(w_0 = 0.7\), \(w_1 = 0.2\)。当然,文档中对于不同的目标函数可能有不同的调参结果,大家可以自行调试。
7.4 优化结果
| Parameter | Description | Values |
|---|---|---|
| \(c\) | Constant | 5 |
| \(\lambda\) | Step length ratio | 0.95 |
| \(\gamma\) | Penalty coefficient | \(10^{50}\) |
| \(n\) | Number of iterations | 1000 |
| \(r\) | Height of crane | 20(m) |
| \(h\) | Load displacement | 40(m) |
| Variables | fmincon | BAS |
|---|---|---|
| \(tp_1\) | 8.9624000 | 6.9082000 |
| \(tp_2\) | 8.9803000 | 6.9741000 |
| \(tf\) | 19.8346000 | 15.8866000 |
| \(f\) | 0.0029586 | 0.0001415 |
从表7.2中可以看到,BAS能够让起重机小车在7秒内加速到最大速度,在16秒内就能到达终点并消除摆角。动图7.3至7.6分别为采用fmincon和BAS做优化的结果,可以让我们有更为直观的认识。
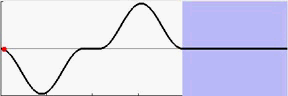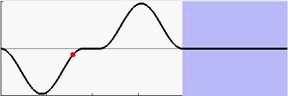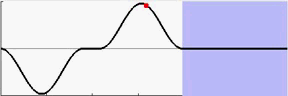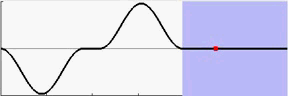
图 7.3: fmincon摆锤
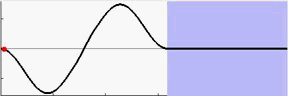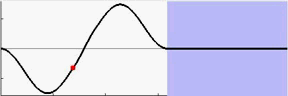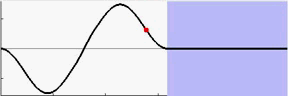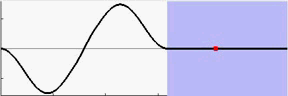
图 7.4: BAS摆锤
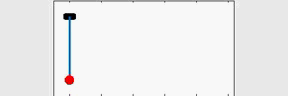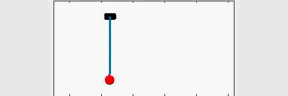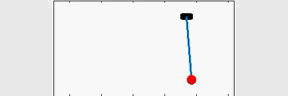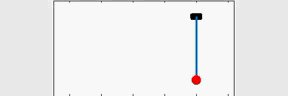
图 7.5: fmincon轨迹
图 7.6: BAS轨迹
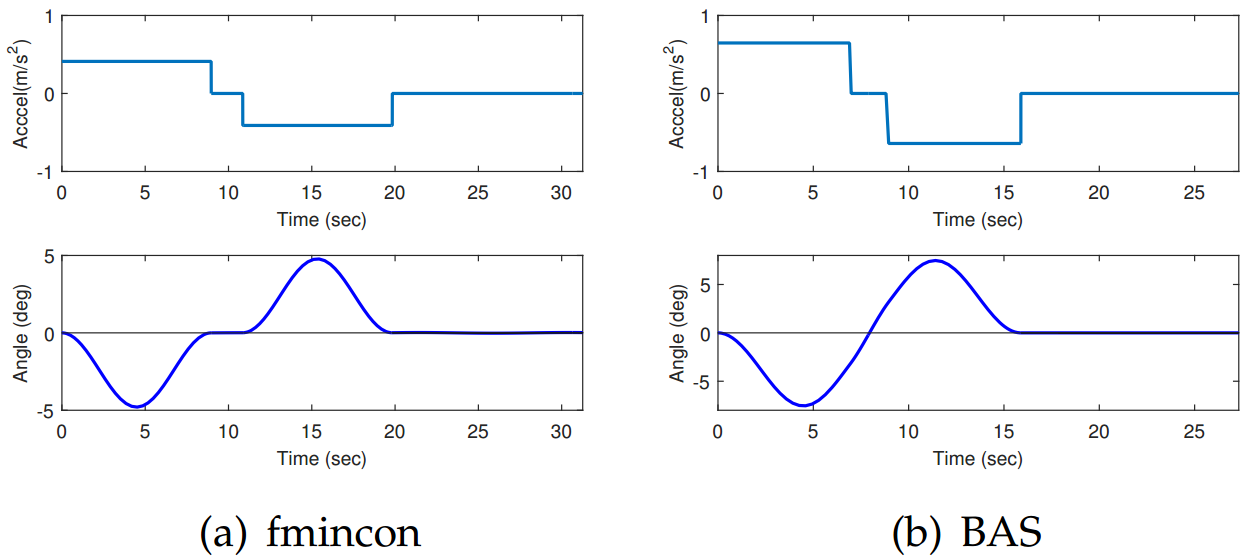
图 7.7: 起重小车加速度曲线
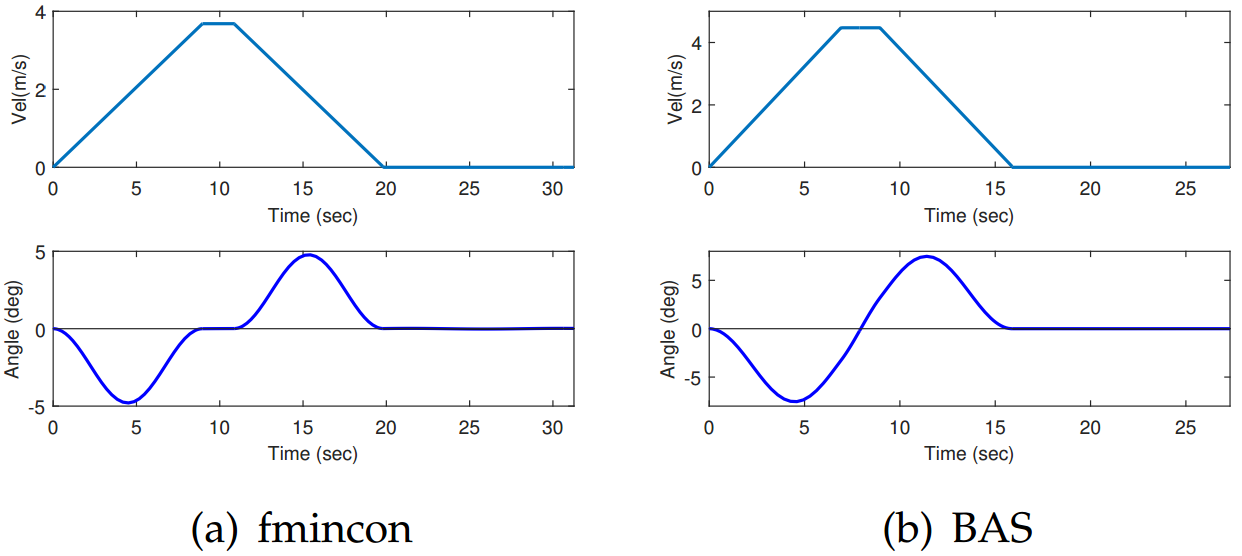
图 7.8: 起重小车速度曲线
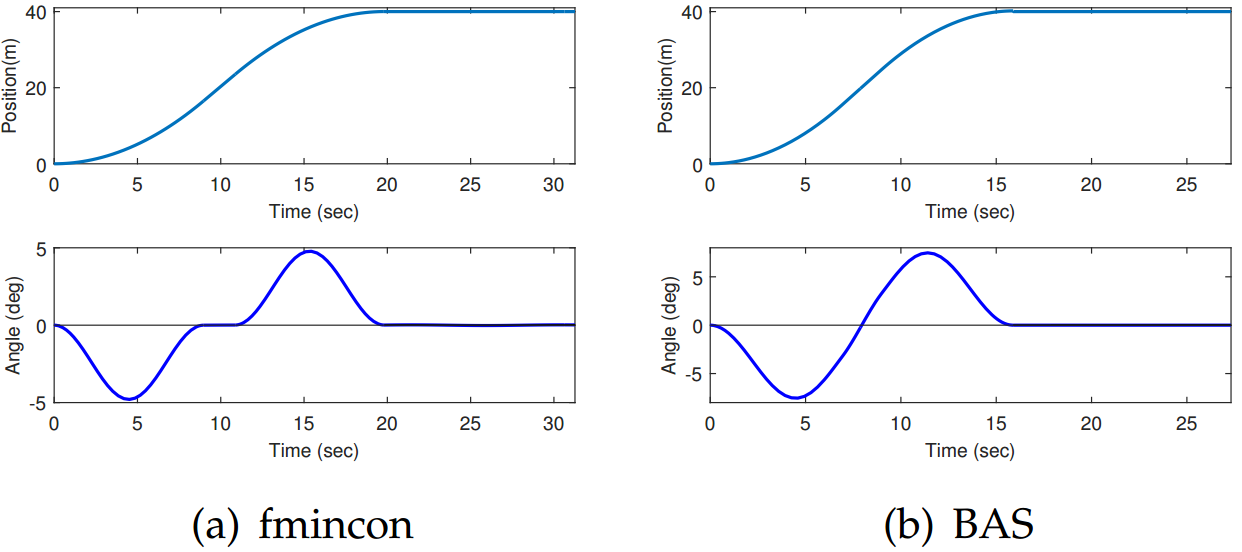
图 7.9: 起重小车位置曲线