第 4 章 函数使用

首先,加载rBAS包，然后在4.1节到4.3节中，我们详细讲述每个参数的含义。如果可能的话，我会加上调参时的经验（可能只对我的问题有用）。

打开网址，可以看到托管在github上的rBAS文档。大家可以通过Reference来访问里面所有函数的帮助文档，通过Changelog来看每次包的更新及bugs修复记录。

文档网页是由pkgdown包制作而成，logo由hexSticker包制作。

4.1 BASoptim/BASoptim2

除了通过访问函数文档网站外，还可以在R中输入下面的命令，来查看文档。

4.1.1 BASoptim参数说明

BASoptim函数(对应BAS算法)调用的格式如下：

直接带有=号的参数，表明是有默认值的。大家可以不指定，但是上下限需要根据实际问题来人为指定。给出的上下限只是因为第一个调试函数是Michalewicz而已。

由于英文蹩脚，所以大家看起包自带的文档会比较吃力。因此，在此处给出中文说明。

  • 已知条件：目标函数与约束
    • fn 待优化的目标函数
    • init 参数初始值，默认为NULL，即在上下限内随机选取，也可以自行指定
    • constr 不等式约束
    • lower/upper 上下限
    • pen 惩罚因子\(\lambda\)
  • BAS待调参数
    • d0 参见式(2.4)中所述的搜索距离（也就是质心到须的距离）参数，一个比较小的值，默认为0.001
    • d1 初始的搜索距离，默认为3
    • eta_d 搜索距离的衰减系数
    • l0/l1/eta_l 这一系列关于\(l\) 的参数，来源于BAS (Jiang Xiangyuan 2017a)论文中给出的matlab代码。其作用在于每回合位置更新时，产生一个随机抖动\(x = x - step * dir * sign(fn(left) - fn(right)) + l *random(npars)\)
    • step/eta_step 步长以及步长的衰减率
    • steptol 停止更新的步长临界值
    • n 回合数或者迭代次数
  • 其他
    • seed 给定随机种子，用来固定寻优结果。不同的种子，对结果的影响非常大。
    • trace 是否显示寻优过程信息

4.1.2 BAS2optim参数说明

BASoptim2函数(对应二阶BAS算法)调用的格式如下：

与前面BASoptim函数调用的大部分参数含义相同。不同点如下：

  • c; \(d = \delta/c\)，\(c\) 是步长 \(\delta\) 与感知距离 \(\d\) 之比。二阶BAS中，不直接指定感知距离。因此，与感知距离相关的参数都被移除。
  • step0; 步长的最小分辨率，可参见式(2.13)。
  • w0;w1;c0分别是式(2.10)中的权重系数，和\(V_{max} = c_0 \delta\)中确定最大速度的系数。

实际调参中，调节w0会给结果带来较大的改变。

4.1.3 BASoptim简单案例

这里采用BAS (Jiang Xiangyuan 2017a)一文中给出的测试函数，即Michalewicz function 与 Goldstein-Price function。

4.1.3.1 Michalewicz function

\[ f(x)=\sum_{i=1}^{d=2}sin(x_i)[sin(\frac{ix_i^2}{\pi})]^{20} \] 图4.1为Michalewicz函数在给定的约束范围的三维示意图。可以看到，最小值在\(x = -5,y = 1.5\)的附近。
Michalewicz函数示意

图 4.1: Michalewicz函数示意

我们先在R的脚本中构建出函数：

然后利用rBAS包中的BASoptim函数求解：

## [1] -4.964687  1.575415
## [1] -1.966817

可以看到，BAS在100个回合内找到了全局的最小值。非R用户可能对上下限的声明有点陌生，c(-6,0)中c()，其实是声明了一个向量，这也是R里面最基本的数据类型，和matlab里面的[-6 0]效果类似。整体看来，代码还是很简洁的。

4.1.3.2 Goldstein-Price function

\[\begin{equation} \begin{split} f({x})=& [1+(x_1+x_2+1)^2(19-14x_1+3x_1^2-14x_2\notag \\ & +6x_1x_2+3x_2^2)][30+(2x_1-3X_2)^2(18-32x_1\notag \\ & +12x_1^2+48x_2-36x_1x_2+27x_2^2)]\notag \end{split} \end{equation}\]

图4.2为Goldstein-Price函数在给定的约束范围的三维示意图。可以看到，最小值在\(x = -5,y = 1.5\)的附近。图4.1与4.2均使用plotly绘制。
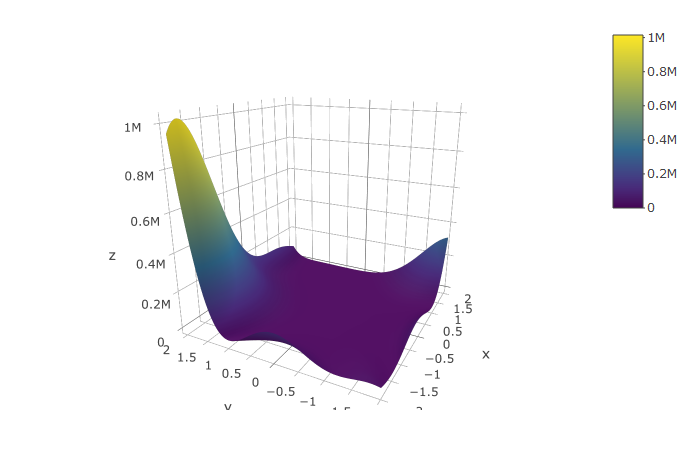
Michalewicz函数示意

图 4.2: Michalewicz函数示意

函数构造：

其中，x[1]表示向量x的第一个元素。举例，x = c(1,2)，那么x[1]等于1，x[2]等于2。索引从1开始，并不是从0开始（python和C++用户可能需要在此处注意）。

优化代码：

## [1]  0.001870855 -0.996496153
## [1] 3.004756

同样，结果也是给出了全局最优点（或在此附近，继续迭代下去，可能会有更精确更小的值）。

4.2 BSASoptim

BSASoptim函数(对应BSAS算法)，在BAS的基础上，加入了步长反馈和群体策略。调用的格式如下：

4.2.1 BSASoptim参数说明

与BAS相比，BSAS在下面几处不同参数：

  • k 每回合的外出试探的天牛数目，越多结果会越稳定(多次执行，结果更接近)，但是计算时长会相应增长。适当选取天牛数目，有助于避免随机的初始值和方向带来影响的同时，计算时长也可以接受。
  • p_min 当k只外出的天牛存在超过1只找到了更优的位置，也就是比当前的最佳值要更小。那是否需要更新到那k只天牛中最优的那一只所在的位置呢？经过一些尝试，我片面地认为，未必是每次都最佳，最后的位置一定最佳。因此，给定一个概率\(p_{min}\)。当有2只或以上的天牛找到更好的位置时，会在[0,1]间生成一个随机数，如果大于\(p_{min}\)，那么就选k只天牛里最优天牛作为下次的更新位置牛；如果小于\(p_{min}\)，那么就在找到了更好的位置的天牛里面，随机选出一只天牛，作为下次的更新位置。
  • p_step 想法与p_min类同，用于控制步长反馈策略。在k只天牛找不到更优位置时，算法认为是步长过大，下一回合天牛位置不更新，且会减小步长。反之，则更新天牛位置，并保持当前步长直至不能找到更优位置。那么，是否存在由于随机方向的原因，或者是k过小，导致在当前步长条件下，存在更优位置，但是找不到。这个时候，我们设置一个更新概率\(p_{step}\)，即在找不到更优的天牛位置下，步长有\(p_{step}\)概率不更新，继续寻找。
  • n_flag 为了防止设定过大的p_step，让数次产生的随机数都小于p_step，影响迭代的效率。我们给定了这个参数，默认为2，只要在同一个步长上的无效搜索(因为找不到更优位置而反复搜索)次数保持3次及以上，则会强制更新步长。

4.2.2 BSASoptim取值摸索

好吧，用中文说明都这么绕口，何况是我撰写的可怜的英文文档。有同学会问了，为什么要后面那几个概率和什么次数的参数，这不是画蛇添足吗？回答是，这几个参数来源于生活···

我在做建筑阻容模型系统辨识时，每回合的寻优，都是在用龙哥库塔法求解一次常微分方程组(ODEs)。在我的问题规模下，每回合纯粹的R代码要耗费0.25s左右来求解一次这样的ODEs。也就是说，在求解目标函数上，程序耗费的时间就有\(k*n*0.25\)，还不算其他的计算开销。（换言之，用遗传算法，会带来更大的计算开销，因为每回合至少计算10*参数个数次的目标函数）

所以，我必须要结果较好的同时，尽量减少不必要的计算。因此，k不能太大，但是这又会在随机方向的影响下，错失一些优化的位置，那就需要p_step参数了。但是初始位置或者说中间位置附近的最优，不代表在这附近或方向上，有全局最优，所以我还需要p_min来保证，我有那么一丝可能，跳出每次都找最优，可是收敛结果与全局最优背离的怪圈。至于n_flag，是因为我之前设置了p_step为0.5，所以算法效率极低，几乎每个找不到更优的夜，这些天牛都悲伤地多做数次运行，所以我设置了这个参数。

还是需要强调，在我的问题里，这些参数起到了较好的效果。但是换成大家的研究，这些参数可能就是被害妄想症的产物了。有意思的是，我在默认参数下执行50次 Michalewicz 函数的寻优，效果并没有BASoptim好。但在RC模型辨识上，BSASoptim远好于BASoptim。

接下来就是这几个参数的调节的一些小技巧了。

  • 设置k为1，那就是带步长反馈的BAS了
  • 如果求解目标函数速度快，可以设置较大的k
  • p_step设置为0，只要k只天牛找不到最优位置，步长就会更新；不存在不更新继续找的可能
  • p_step设置为1，那算法会在一个步长下一直执行，直到找到更优的位置，才会更新步长
  • p_min设置为0，在k只出去试探的天牛中找到了更优的位置时，那么当前时刻的天牛，总会选择这k只中最好的一只的位置来作为下一时刻的位置
  • p_min设置为1，下一时刻的位置是k只中更优天牛的位置的随机选择
  • 为了求解效率，p_step会选择较小的值；p_min我也没有摸清楚个规律，但是在我的研究对象中，为0得到的结果在多次试验中，整体看来没有为较小值0.2好。

上述是我在自身研究方向上摸出的规律，可能问题的类型不同，需要做的取舍也不同。大家可以保持默认参数，然后进行符合自身情况的微调。更为详细的结果可以参见BSAS (Wang Jiangyu 2018)论文。

4.2.3 BSASoptim案例

4.2.3.2 Pressure Vessel function

使用BAS-WPT(Jiang Xiangyuan 2017b) 论文中压力容器优化函数来测试BSASoptim处理约束的能力。问题背景如下：

\[\begin{align} \text{minimize} f(\mathbf{x}) = &0.6224x_1x_3x_4+1.7781x_2x^2_3 \notag\\ &+3.1661x^2_1x_4 + 19.84x^2_1x_3 \notag \\ s.t. ~~ g_1(\mathbf{x}) = & -x1 + 0.0193x_3 \leq 0 \notag \\ g_2(\mathbf{x}) = & -x_2 + 0.00954x_3 \leq 0 \notag \\ g_3(\mathbf{x}) = & -\pi x^2_3x_4 -\frac{4}{3}\pi x^3_3 + 1296000 \leq 0 \notag \\ g_4(\mathbf{x}) = & x_4-240\leq 0 \notag \\ x_1 \in& \{1,2,3,\cdots,99\}\times0.0625 \notag \\ x_2 \in& \{1,2,3,\cdots,99\}\times0.0625 \notag \\ x_3 \in& [10,200] \notag \\ x_4 \in& [10,200] \notag \\ \tag{4.1} \end{align}\]

构造一个列表，也就是list()。其中包含有2个函数，一个是我们的目标函数obj，一个是我们的不等式约束函数con。为了方便起见，我并没有写每一个函数的返回值，那么，R会自动返回计算的最后一个对象。比如，在obj函数中，是result变量（标量）被返回。而在con函数中，是由c()声明的向量被返回。

使用BSASoptim函数进行优化。需要注意的是,pressure_Vessel是一个列表，对于其中包含的元素，使用$符号进行访问。也可以使用[[符号，即 pressure_Vessel$obj 等价于 pressure_Vessel[[1]]。

## [1]  14.92195   7.87620  43.51377 159.87104
## [1] 6309.406

可以看到结果与论文BAS-WPT(Jiang Xiangyuan 2017b)中TABLE 1给出的优化值还是有一定的差距。不过，这也让我意识到了，对于复杂的优化问题，调试其中的参数是个困难的活。歧路亡羊呀！

好在，改进后的BSAS-WPT能够比较好地得到不逊于BAS-WPT(Jiang Xiangyuan 2017b)中的结果（在4.3.2节可以看到）。更多更优地结果，等待你去调参，如果你还有勇气的话。

4.2.3.3 Himmelblau function

\[\begin{align} \text{minimize} f(\mathbf{x}) =& 5.3578547x^2_3 +0.8356891x_1x_5\notag \\ &+ 37.29329x_1 - 40792.141 \notag\\ s.t. ~~g_1(\mathbf{x}) =& 85.334407 + 0.0056858x_2x_5\notag\\ &+ 0.00026x_1x_4 - 0.0022053x_3x_5 \notag\\ g_2(\mathbf{x}) =&80.51249 +0.0071317x_2x_5\notag\\ &+ 0.0029955x_1x_2 + 0.0021813x^2_3 \notag\\ g_3(\mathbf{x}) =& 9.300961 +0.0047026x_3x_5\notag\\ &+ 0.0012547x_1x_3 + 0.0019085x_3x_4 \notag\\ g_1(\mathbf{x})\in&[0,92] \notag\\ g_2(\mathbf{x})\in&[90,110] \notag\\ g_3(\mathbf{x})\in&[20,25] \notag\\ x_1\in&[78,102] \notag\\ x_2\in&[33,45] \notag\\ x_3\in&[27,45] \notag\\ x_4\in&[27,45] \notag\\ x_5\in&[27,45] \notag\\ \tag{4.2} \end{align}\]

构造优化目标函数和约束：

使用BSASoptim函数进行优化：

## [1] 78.01565 33.00000 27.07409 45.00000 44.95878
## [1] -31024.17

这个结果，比BAS-WPT(Jiang Xiangyuan 2017b)中TABLE 2记载的结果要好，但与参数设置关系较大。

4.3 BSAS-WPT

在进行BSAS-WPT参数讲解的这一部分前，我想问个问题。在式(4.1)和式(4.2)中，我们可以看到，有些\(x_i\)的约束范围较小，有的较大。比如，压力容器中，\(x_1\)和\(x_2\)就偏小，只是经过提取出0.0625，勉强能达到\(x_3\)和\(x_4\)的一半。那么，如果某些优化问题，其参数约束范围之间，相差了量级，该如何选择步长呢？这就是WPT的便捷之处了。

BSAS-WPT函数(对应BSAS-WPT算法)调用的格式如下：

4.3.1 BSAS-WPT 参数说明

与BSAS相比，除去我人为略去的抖动部分，减少了搜索距离d相关的参数，这些用c2来替代。而初始步长step，我们可以设定为一个在1附近的数。由于算法先标准化了参数，然后根据式(2.3)在计算位置后，再根据上下限进行反标准化，而后导入目标函数。所以，你可以认为，BSAS中，把step变成一个\(n\)维的向量，假设\(n\)是参数个数，每个步长元素都根据参数的约束范围大小来设定，那么算法就会变成BSAS-WPT。

总之，现在要调节的参数，主要有2个，即c2和step。

4.3.2 BSAS-WPT 案例

我们使用和BSASoptim函数相同的例子来对比效果。但是，这些效果都是不固定的，即给定不同的参数，结果也会不同，所以不能根据一次结果评价算法的优劣。

4.3.2.2 Himmelblau function

## ----step < steptol---------stop the iteration------
## [1] 78.00000 33.00000 27.07176 45.00000 44.96713
## [1] -31025.47

BSAS-WPT没有做过多的参数调节，即可获得更畅快地优化体验。举例，在对Himmelblau函数进行优化时，我仅仅设定了随机种子seed，然后把step从1调到了2，看了看效果的变化。发现都不错，最后每隔0.1选取step，试探最好的效果在哪里，于是就成了上面的例子。 如果把这一套，放在BSASoptim函数上，对于复杂的优化问题，就成了一种折磨。

4.4 BSOoptim

4.4.1 BSO参数说明

由于BSO参数与原理中的公式较为复杂。因此，在讲述其原理时，对函数的参数也进行了说明。故大家可以参考3.1.4节。此处，仅仅复制该节内容。

上面的代码是函数的默认调用形式，其中\(s\)表示设定的天牛或者粒子数目，\(w\)也就是式(3.3)中提到的\(\omega_{max}\)和\(\omega_{min}\)。w_vs 是\(\lambda\)，也就是式(3.4)中天牛速度和移动步长之间的权重，直观地理解为weight between velocity and step-size。step和c仍然是表示步长和步长与须距离之比。而\(step_w\)为一个向量，表示的是式(3.7)中的\(\omega_{\delta_1} = 0.4\)， \(\omega_{\delta_0} = 0.9\)。

4.4.2 BSO案例

4.4.2.2 Pressure Vessel function

## [1]  13.955250   7.550179  42.098446 176.636596
## [1] 6059.131

得到的结果十分好（甚至比论文(Wang Tiantian 2018)还要高出那么一点点）。但是，这是调参调出来的结果。

总的来说，我自己的经验是：

  • 调节最大迭代次数n
  • 调节步长step和步长与须距离比值c（让搜索距离的尺度尽量在迭代后不要太大）
  • 调节w_vs，该值越大，粒子群算法更新方式所占的比重越大。

而王糖糖同学给出的建议是：

“在试验的时候发现，当维度提高时，步长和迭代次数也要相应的提高”

—王糖糖

4.5 bBAS

4.5.1 bBAS参数说明

bBAS算法原理参看 3.2 节。 对应的bBASoptim函数，与其他算法相比，需要调节的参数较少。调用形式如下。

\(w\) 与 \(c\) 分别为式(3.9)与式(3.10)中的惯性项与常系数。 \(vmax\) 则用于控制速度的边界。

trace参数表示，每隔多少次循环，打印一次结果。

resolution 则是我们在处理实数空间优化问题时候所给的分辨率。这么说有点绕口，举例说明。如果Michalewicz function使我们的优化目标，上下限分别是 (-6,0)和(-1,2)。

那问题来了，用二进制数来模拟取值空间：

  • 我们如何让二进制数取负数呢？
  • 我们如何让二进制数取小数呢？

首先，算法把 \(x_1\in[-6,-1]\) 转为\(x_1\in[0,5]\) 来处理。然后新的空间转为二进制后，可以写作\(x_1 \in [000,101]\)，\(x_2 \in [00,10]\)。也就是，表示第一个分量，需要三个二进制位，表示第二个分量，需要两个二进制位，然后我们的算法就可以对于每个二进制位的0-1进行寻优调节。但是实际上的二进制上限会与十进制的值有所出入，可能会出现 \(x_1 = 111, x_2 = 11\)的状况。

大家可能会问，为什么不进行上下限的判定？主要是因为还没有想好，如果超过上下限，该限制哪些位数上的取值。此外，二进制转十进制判断大小，会拖慢循环的速度。所以，下面有个更好的办法。

因此，我们只在转二进制后只获取和关注位数信息，把新的范围写为 \(x_1\in[000,111], x_2\in[00,11]\) ，也就是上限全部位数为1，下限全部位数为0。然后利用下面的方法来变成原来的实数空间的取值。

\[ \begin{aligned} x_1 &= \frac{x_{1,binary}-0}{(2^3-1)-0} * (-1-(-6))\\ x_0 &= \frac{x_{0,binary}-0}{(2^2-1)-0} * (2-(0))\\ \end{aligned} \] 这样，就不用担心在取值的过程中，溢出上下限了。

接下来，问题又来了，这样的表示方法，能够搜索到的值寥寥无几。我们可以穷举出来， \(x1\in\frac{5}{2^3-1}*k\quad k=0,1,\cdots,7\) ，共8种取值，而 \(x_2\) 共4种取值。所以，如果搜索空间只有32种可能，这肯定是不合理的，我们需要更细的粒度来让算法更为细致地搜索参数空间。这就是分辨率参数的由来。

还是上面的问题，取值范围有限是由于二进制位数小引起的，二进制位数小是由于十进制的上下限差距小引起的。换言之，我们可以考虑放大参数的上下限。 比如，我们使用100的分辨率（倍数），那么 \(x_1\in[-600,-10] = [0,590] = [0000000000,1001001110]\) ,现在，二进制位数变为了10位，当然，还会稍作扩大，使得 \(x_1\) 新的上限为1111111111。而 \(x2\) 的取值为 \(x_2\in[0,200]=[00000000,11001000]\) , 二进制位变为了8位。同样，按照下面的方式转为原始空间的取值。

\[ \begin{aligned} x_1 &= \frac{x_{1,binary}-0}{(2^{10}-1)-0} * (-1-(-6))\\ x_0 &= \frac{x_{0,binary}-0}{(2^{8}-1)-0} * (2-(0))\\ \end{aligned} \]

这样，我们能探索的空间有 \(2^{10}*2^8\)种可能性，这样能极大地增大寻优的几率。把分辨率理解为，你要精确到小数点后多少位。比如 \(x\in[-2.048,2.048]\)，设置1000的分辨率，表明希望能精确到0.001位。当然，这是比较形象的一个理解办法。

一个小的技巧是，对于库存问题，参数本身的取值就是0和1，那么分辨率设为1即可，这也是默认取值；而对于实数空间的取值，如[-2.048,2.048]，可以设置分辨率为1000。**如果参数中既有0-1变量，又有实数变量，可以分别设置，比如 \(x_1 = 0,1 \quad x_2\in[-1,1]\)，可以设置分辨率为 resolution = c(1,100)。

4.5.2 bBAS案例

对于上面提及的Michalewicz function 优化问题，代码如下：

## Iters 0 xbest = [ -3 1 ], fbest = -2.55738e-05 
## Iters 20 xbest = [ -3.651663 1.607843 ], fbest = -0.9949117 
## Iters 40 xbest = [ -4.581213 1.568627 ], fbest = -0.9998098 
## Iters 60 xbest = [ -4.581213 1.568627 ], fbest = -0.9998098 
## Iters 80 xbest = [ -4.581213 1.568627 ], fbest = -0.9998098 
## Iters 100 xbest = [ -3.78865 1.458824 ], fbest = -1.111469 
## Iters 120 xbest = [ -3.798434 1.537255 ], fbest = -1.485165 
## Iters 140 xbest = [ -3.798434 1.537255 ], fbest = -1.485165 
## Iters 160 xbest = [ -3.798434 1.537255 ], fbest = -1.485165 
## Iters 180 xbest = [ -3.798434 1.537255 ], fbest = -1.485165 
## Iters 200 xbest = [ -3.798434 1.537255 ], fbest = -1.485165 
## Iters 220 xbest = [ -3.798434 1.537255 ], fbest = -1.485165 
## Iters 240 xbest = [ -3.798434 1.537255 ], fbest = -1.485165 
## Iters 260 xbest = [ -3.798434 1.537255 ], fbest = -1.485165 
## Iters 280 xbest = [ -3.798434 1.537255 ], fbest = -1.485165 
## Iters 300 xbest = [ -3.798434 1.537255 ], fbest = -1.485165 
## Iters 320 xbest = [ -3.798434 1.537255 ], fbest = -1.485165 
## Iters 340 xbest = [ -3.798434 1.537255 ], fbest = -1.485165 
## Iters 360 xbest = [ -3.798434 1.537255 ], fbest = -1.485165 
## Iters 380 xbest = [ -5.011742 1.6 ], fbest = -1.747737 
## Iters 400 xbest = [ -5.011742 1.6 ], fbest = -1.747737 
## Iters 420 xbest = [ -5.011742 1.6 ], fbest = -1.747737 
## Iters 440 xbest = [ -5.011742 1.6 ], fbest = -1.747737 
## Iters 460 xbest = [ -5.011742 1.6 ], fbest = -1.747737 
## Iters 480 xbest = [ -5.011742 1.6 ], fbest = -1.747737 
## Iters 500 xbest = [ -5.011742 1.6 ], fbest = -1.747737 
## Iters 520 xbest = [ -5.011742 1.6 ], fbest = -1.747737 
## Iters 540 xbest = [ -5.011742 1.6 ], fbest = -1.747737 
## Iters 560 xbest = [ -5.011742 1.6 ], fbest = -1.747737 
## Iters 580 xbest = [ -5.011742 1.6 ], fbest = -1.747737 
## Iters 600 xbest = [ -5.011742 1.6 ], fbest = -1.747737 
## Iters 620 xbest = [ -4.972603 1.537255 ], fbest = -1.919954 
## Iters 640 xbest = [ -4.972603 1.537255 ], fbest = -1.919954 
## Iters 660 xbest = [ -4.972603 1.568627 ], fbest = -1.963422 
## Iters 680 xbest = [ -4.972603 1.568627 ], fbest = -1.963422 
## Iters 700 xbest = [ -4.972603 1.568627 ], fbest = -1.963422 
## Iters 720 xbest = [ -4.972603 1.568627 ], fbest = -1.963422 
## Iters 740 xbest = [ -4.972603 1.568627 ], fbest = -1.963422 
## Iters 760 xbest = [ -4.972603 1.568627 ], fbest = -1.963422 
## Iters 780 xbest = [ -4.972603 1.568627 ], fbest = -1.963422 
## Iters 800 xbest = [ -4.972603 1.568627 ], fbest = -1.963422
## [1] -4.972603  1.568627
## [1] -1.963422

此处还有阮月同学提供的库存(批次)问题(lot-sizing)案例。

\[\begin{align} \text{minimize} &\sum_{i=1}^n(Ax_i+cI_i) \notag\\ s.t. ~~ &I_0 = 0 \notag \\ &I_{i-1}+x_iQ_i-I_i=R_i \notag \\ &I_i\geq 0 \notag \\ &Q_i\geq 0 \notag \\ &x_i \in{0,1}\notag \\ \tag{4.3} \end{align}\]

该案例具体的参数解释会在之后案例章节描述。此处简单给出例子。

## Iters 0 xbest = [ 1 1 1 1 1 ], fbest = 500 
## Iters 10 xbest = [ 1 0 0 1 1 ], fbest = 440 
## Iters 20 xbest = [ 1 0 0 1 0 ], fbest = 420 
## Iters 30 xbest = [ 1 0 0 1 0 ], fbest = 420 
## Iters 40 xbest = [ 1 0 0 1 0 ], fbest = 420 
## Iters 50 xbest = [ 1 0 0 1 0 ], fbest = 420 
## Iters 60 xbest = [ 1 0 0 1 0 ], fbest = 420 
## Iters 70 xbest = [ 1 0 1 0 1 ], fbest = 410 
## Iters 80 xbest = [ 1 0 1 0 1 ], fbest = 410 
## Iters 90 xbest = [ 1 0 1 0 1 ], fbest = 410 
## Iters 100 xbest = [ 1 0 1 0 1 ], fbest = 410 
## Iters 110 xbest = [ 1 0 1 0 1 ], fbest = 410 
## Iters 120 xbest = [ 1 0 1 0 1 ], fbest = 410 
## Iters 130 xbest = [ 1 0 1 0 1 ], fbest = 410 
## Iters 140 xbest = [ 1 0 1 0 1 ], fbest = 410 
## Iters 150 xbest = [ 1 0 1 0 1 ], fbest = 410 
## Iters 160 xbest = [ 1 0 1 0 1 ], fbest = 410 
## Iters 170 xbest = [ 1 0 1 0 1 ], fbest = 410 
## Iters 180 xbest = [ 1 0 1 0 1 ], fbest = 410 
## Iters 190 xbest = [ 1 0 1 0 1 ], fbest = 410 
## Iters 200 xbest = [ 1 0 1 0 1 ], fbest = 410
## [1] 1 0 1 0 1
## [1] 410

得到的结果能使得库存与订单总的费用最小。

表 4.1: 需求订单与库存
day1 day2 day3 day4 day5 \(f(X^k)\)
\(R_d\) 100 60 40 50 80 -
\(x_d^k\) 1 0 1 0 1 -
\(Q_d^k\) 160 - 90 - 80 -
\(I_d^k\) 60 - 50 - - -
\(c_d^k\) 60 - 50 - - -
\(Ax_d^k\) 100 - 100 - - -
\(C(X_d^k)\) 160 - 150 - 100 410

References

Jiang Xiangyuan, Li Shuai. 2017a. “BAS: Beetle Antennae Search Algorithm for Optimization Problems.” arXiv.

Jiang Xiangyuan, Li Shuai. 2017b. “Beetle Antennae Search Without Parameter Tuning (Bas-Wpt) for Multi-Objective Optimization.” arXiv.

Wang Jiangyu, Chen Huanxin. 2018. “BSAS: Beetle Swarm Antennae Search Algorithm for Optimization Problems.” arXiv.

Wang Tiantian, Liu Qiang, Yang Long. 2018. “Beetle Swarm Optimization Algorithm:Theory and Application.” arXiv.