第 6 章 BAS案例一:多杆机构优化问题

说明：由于自身专业知识局限，在整理转述各位研究者或贡献者所提供的材料时，我可能无法准确地表达出对应领域的知识要点。避免言多必失，我仅仅做简要的翻译或者是介绍。对于读者而言，如果觉得并不能解你之疾，或没有挠到痒处，建议直接和对应的作者联系。对于贡献者而言，如果我表述有误，欢迎提出建议，或者在github上pull request。

由群友莫小娟博士研究生提供案例。

由于案例均为各位热心的同学提供，均为自己的研究。因此，希望大家要引用其中的结果时，可以引用对应同学的文章。此外，也请大家转载时注明来源。

6.1 背景

6.1.1 四连杆机构(Four-bar linkage mechanism)

四连杆机构如图6.1所示：

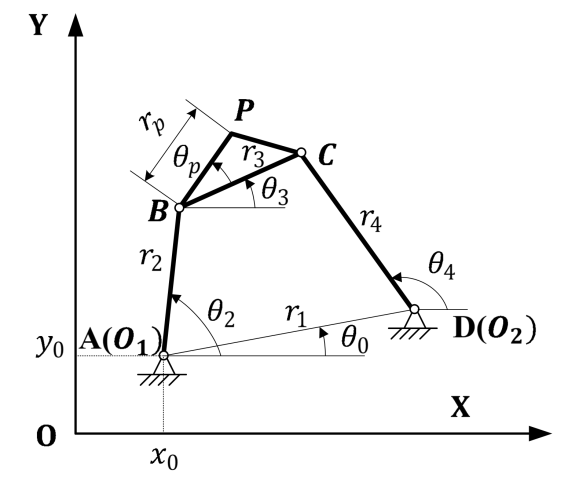
四连杆机构示意

图 6.1: 四连杆机构示意

基于闭环矢量方程，推导出节点位置。推导过程如式(6.1)至式(6.4):

\[\begin{equation} \mathbf{\text{Loop:}} r_1e^{i\theta_0} + r_4e^{i\theta_4} - r_2e^{i\theta_2} -r_3e^{i\theta_3} = 0\\ \tag{6.1} \end{equation}\]

\[\begin{equation} \begin{cases} r_1cos(\theta_0) + r_4cos(\theta_4)-r_2cos(\theta_2)-r_3cos(\theta_3)=0 \\ r_1sin(\theta_0) + r_4sin(\theta_4)-r_2sin(\theta_2)-r_3sin(\theta_3)=0 \end{cases} \tag{6.2} \end{equation}\]

\[\begin{equation} \begin{split} &\theta_3 =2atan(\frac{-A\pm\sqrt{2}{A^2-4BC}}{2B})+\theta_0\\ &A = cos(\theta_2 - \theta_0)-K_1+K_2cos(\theta_2-\theta_0)+K_3\\ &B = -2sin(\theta_2-\theta_0), F=K_1+(K_2-1)cos(\theta_2-\theta_0)+K_3\\ &K_1 = r_1/r_2,K_2=r_1/r_3,K_3=(r_4^2-r_1^2-r_2^2-r_3^2)/(2r_2r_3)\\ \end{split} \tag{6.3} \end{equation}\]

\[\begin{equation} \begin{cases} x_p=x_0+r_2cos(\theta_2)+r_pcos(\theta_3+\theta_p) \\ y_p=y_0+r_2sin(\theta_2)+r_psin(\theta_3+\theta_p) \end{cases} \tag{6.4} \end{equation}\]

6.1.2 六连杆机构(Stephenson III Six-bar linkage mechanism)

六连杆机构如图6.2所示：

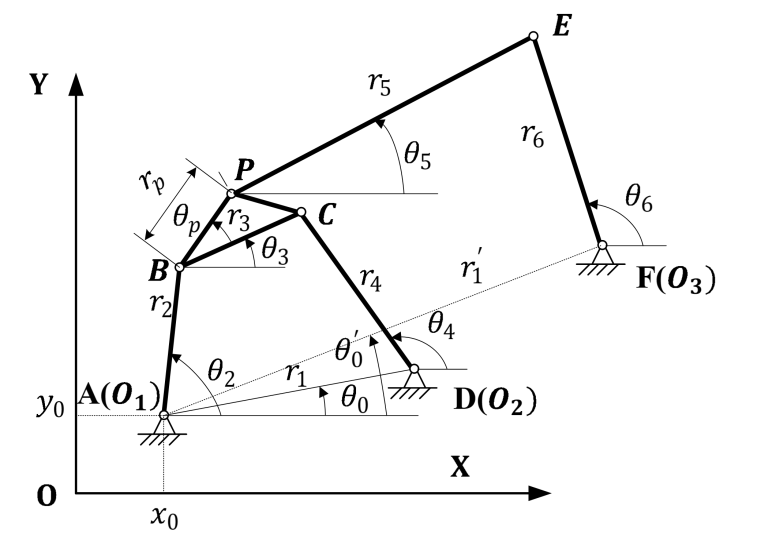
六连杆机构示意

图 6.2: 六连杆机构示意

基于闭环矢量方程，推导出节点位置和外部链接角度。推导过程如式(6.5)至式(6.6):

\[\begin{equation} \begin{split} &\mathbf{\text{Loop1:}} r_1e^{i\theta_0} + r_4e^{i\theta_4} - r_2e^{i\theta_2} -r_3e^{i\theta_3} = 0\\ &\mathbf{\text{Loop2:}} r_1'e^{i\theta_0'} + r_6e^{i\theta_6} - r_2e^{i\theta_2} -r_pe^{i(\theta_3+\theta_p)}-r_5e^{i\theta_5} = 0\\ \end{split} \tag{6.5} \end{equation}\]

\[\begin{equation} \begin{split} \text{Loop1:}\\ &\alpha = r_2cos(\theta_2) - r_1cos(\theta_0), \beta = r_2sin(\theta_2)-r_1sin(\theta_0) \\ &\gamma = (r_4^2+\alpha^2+\beta^2-r_3^2)/(2r_4),\lambda=atan2(\alpha,\beta)\\ &\theta_4 = atan(cos(\lambda)\gamma/\beta,\{1-(cos(\lambda)\gamma/\beta)^2\}^{1/2})-\lambda\\ &\theta_3=atan2(r_4sin(\theta_4)-\beta,r_4cos(\theta_4)-\alpha)\\ \text{Loop2:}\\ &\alpha_1 = r_2cos(\theta_2)+r_pcos(\theta_3+\theta_p)-r_6cos(\theta_6)\\ &\beta_1=r_2sin(\theta_2)+r_psin(\theta_3+\theta_p)-r_6sin(\theta_6)\\ &\gamma_1=(r_6^2+\alpha_1^2+\beta_1^2-r_5^2)/(2r_6),\lambda_1=atan2(\alpha_1,\beta_1)\\ &\theta_6=atan2(cos(\lambda)\gamma_1/\beta_1,-\{1-(cos(\lambda_1)\gamma_1/\beta_1)^{2}\}^{1/2}) - \lambda_1\\ &\theta_5 = atan2(r_6sin(\theta_6)-\beta_1,r_6cos(\theta_6)-\alpha_1) \end{split} \tag{6.6} \end{equation}\]

于是，可以得到节点位置如式(6.7)：

\[\begin{equation} \begin{cases} x_A = x_0,y_A = y_0 \\ x_D = x_0+r_1cos(\theta_0),y_D = y_0+r_1sin(\theta_0)\\ x_F = x_0+r_1'cos(\theta_0'),x_F = x_0 + r_1'sin(\theta_0')\\ x_p = x_0 + r_2cos(\theta_2) + r_pcos(\theta_3+\theta_p)\\ y_P = y_0 + r_2sin(\theta_2)+r_Psin(\theta_3+\theta_p)\\ \end{cases} \tag{6.7} \end{equation}\]

6.2 优化问题

6.2.1 四连杆机构

四杆机构的优化问题可以用式(6.8)表示。

\[\begin{equation} \begin{split} \text{min } &\sum_{i=1}^N[(P_{Xd}^i-P_X^i)^2+(P_{Yd}^i-P_Y^i)^2]+M_1h_1(x)+M_2h_2(x)\\ \text{where } & x_i\in [l_{min}^i,l_{max}^i] \quad \forall x_i \in X,\\ &X=[r_1,r_2,r_3,r_4,r_p,\theta_p,\theta_0,x_0,y_0,\theta_2^1,\cdots,\theta_2^N]\\ \end{split} \tag{6.8} \end{equation}\]

其中，

\[\begin{equation} h_1(x) = \begin{cases} 1, & \text{the Grashof condition false}\\ 0, & \text{the Grashof condition true} \end{cases} \tag{6.9} \end{equation}\]

\[\begin{equation} h_2(x) = \begin{cases} 1, & \text{the sequence condition of the crank angle false}\\ 0, & \text{the sequence condition of the crank angle true} \end{cases} \tag{6.10} \end{equation}\]

\(h_1(X)\) 和 \(h_2(X)\) 分别用于评估曲柄存在条件（Grashof Condition）以及曲柄角度（顺时针或逆时针）的顺序情况。\(M_1\) 和 \(M_2\)分别是对应的惩罚系数。\(X\) 为设计参数。

6.2.2 六连杆机构

\[\begin{equation} \begin{split} \text{min } &\sum_{i=1}^N[(P_{Xd}^i-P_X^i)^2+(P_{Yd}^i-P_Y^i)^2]+\sum_{i=1}^M[(\theta_{6d}^i-\theta_6^i)^2]\\ &+M_1h_1(x)+M_2h_2(x)+M_3h_3(X)\\ \text{where } & x_i\in [l_{min}^i,l_{max}^i] \quad \forall x_i \in X,\\ &X=[r_1,r_2,r_3,r_4,r_5,r_6,r_p,\theta_p,\theta_0,x_0,y_0,\theta_2^1,\cdots,\theta_2^N]\\ \end{split} \tag{6.11} \end{equation}\]

其中，\(h_1(X)\) 与 \(h_2(X)\) 同式(6.9)与(6.10)， \(h_3(X)\)如式(6.12)：

\[\begin{equation} h_3(x) = \begin{cases} 1, & \text{non-violation of transmission angle false}\\ 0, & \text{non-violation of transmission angle true} \end{cases} \tag{6.12} \end{equation}\]

\(h_3(X)\) 所表示的是，是否没有违背传动角（超过20°）的约束。同样地，\(M_3\) 为对应的惩罚系数。

6.3 优化理论

案例所使用的算法是标准化的群体天牛算法。有意思的是，此处群体天牛算法，和rBAS包的BSASoptim的算法极为类似。这也说明，加入群体智能策略，会使得BAS对于复杂问题寻优能力增强。

联系在于：此案例使用的群体天牛，是在每回合，对于天牛探索方向数的提升。即，每回合生成多个随机的方向，在这些方向上，派出天牛进行试探。这点和BSAS保持一致，可以理解为，如果天牛不止有一对须，而是有多对，那每回合探索的方向也会有多个。大致的原理如式(6.13)：

\[\begin{equation} \begin{split} x_{ri} &= x_{t} + d^t\overrightarrow{b_i}, \quad i = 1,\cdots,q\\ x_{li} &= x_{t} - d^t\overrightarrow{b_i}, \\ x_{ti} &= x_{t-1} - \delta^t\overrightarrow{b_i}sign(f(x_{ri})-f(x_{li})) \end{split} \tag{6.13} \end{equation}\]

区别在于：并未使用基于结果反馈的步长调节策略。

对于轨迹优化问题，莫小娟同学给出的参数建议是，\(d_0 = 0.10,\delta_0=0.05,c_1=0.9998,c_2=0.5,q=40,T_{max}=50000\)。部分同学可能看过手册的2节，对于步长\(d\)和须到质心距离\(\delta\)的更新，即式(2.6)中有所提及。此处，参数的含义如式(6.14)所示。部分参数与式(2.6)类同，也有同名但含义冲突的，大家复现时需要注意这些地方。

\[\begin{equation} \begin{split} d^t &= c_1d^{t-1}\\ \delta^t&=c_2 d^t\\ \end{split} \tag{6.14} \end{equation}\]

6.4 优化结果

此处，莫小娟同学提供了8个案例，并且与其他的经典算法（指多杆机构优化问题中多用的算法）进行了优化效果的对比。

6.4.1 Case1 无规定时间内轨迹生成(Path generation without prescribed timing)

本案例是四杆机构的路径（6个点）在一条垂直的线上（没有规定时间）。通过式(6.8)计算得到误差。

设计参数为：

\[ X = [r_1,r_2,r_3,r_4,r_p,\theta_p,\theta_0,x_0,y_0,\theta_2^1,\cdots,\theta_2^6] \] 目标点坐标：

\[ \{C_d^i\} = \{(20,20),(20,25),(20,30),(20,40),(20,45)\} \]

参数约束：

\[ r_1,r_2,r_3,r_4\in[0,60]\quad r_p,x_0,y_0\in[-60,60]\quad \theta_0,\theta_1,\cdots,\theta_2^6,\theta_p\in[0,2\pi] \] 算法参数为 \(d_0 = 0.10,\delta_0=0.05,c_1=0.9998,c_2=0.5,q=40,T_{max}=50000\)，动画结果如图6.3。

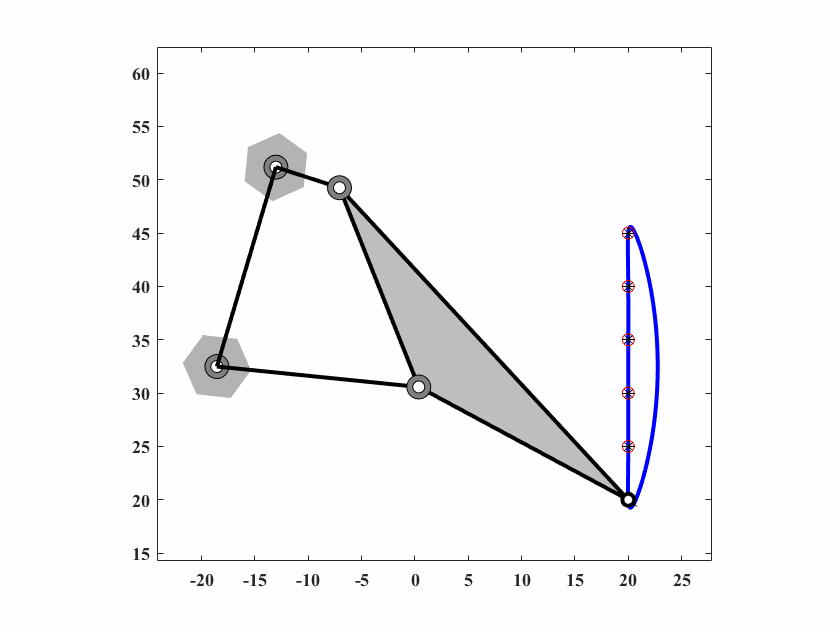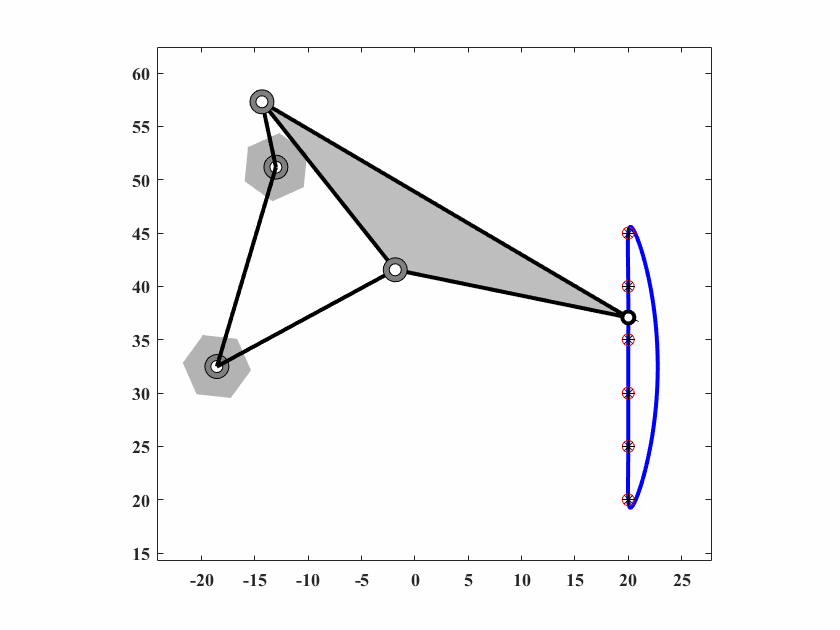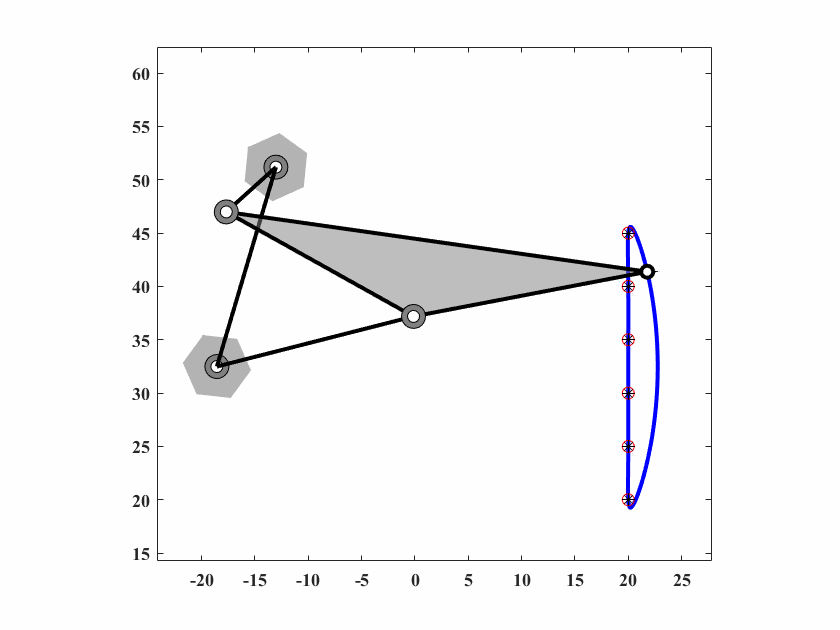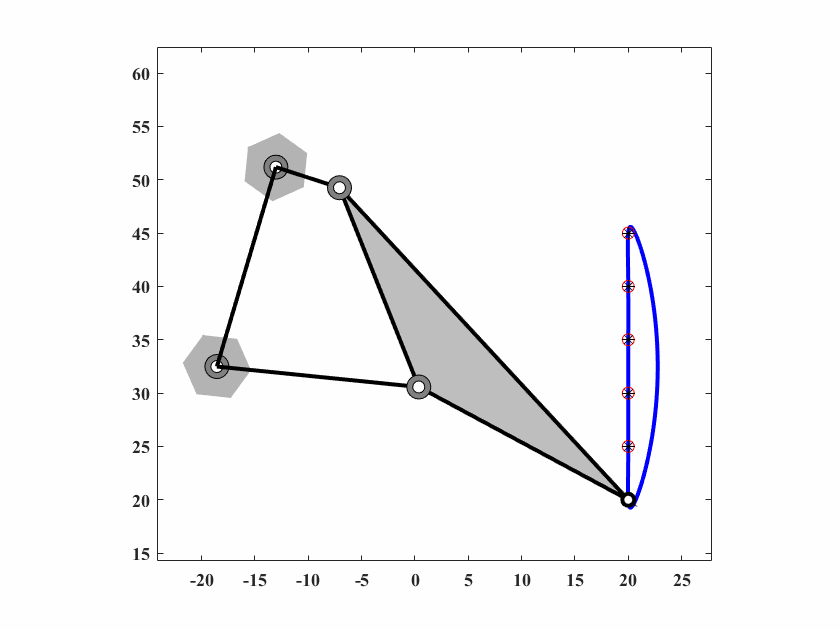
四杆机构轨迹生成

图 6.3: 四杆机构轨迹生成

与其他算法对比结果如图6.4和表6.1。

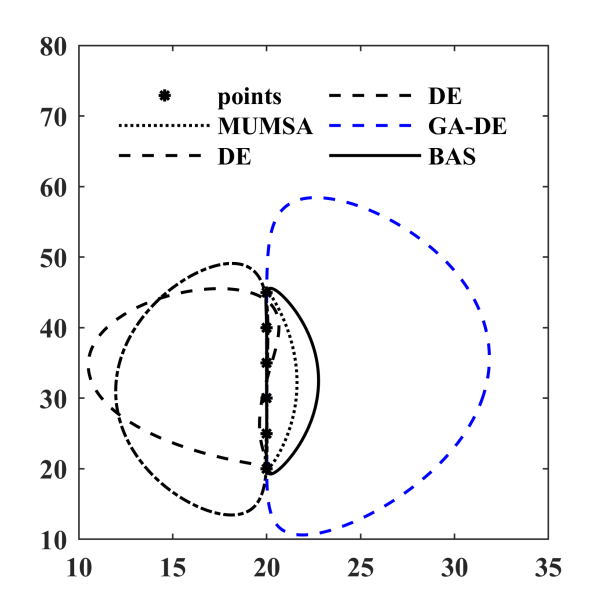
各算法优化轨迹

图 6.4: 各算法优化轨迹

表 6.1: case1各算法结果对比
MUMSA GA DE GA.DE BAS
\(r_1\) 31.788264 28.771330 35.020740 13.2516000 19.4920810
\(r_2\) 8.204647 5.000000 6.404196 5.9407800 6.2644716
\(r_3\) 24.932131 35.365480 31.607220 58.3118000 20.1001631
\(r_4\) 31.385926 59.136810 50.599490 53.7207000 19.0219161
\(r_p\) 37.108246 14.850370 46.461261 61.3011560 39.8538048
\(\theta_p\) 0.398977 1.570796 1.106544 -1.3002600 0.3679660
\(\theta_0\) 4.015959 5.287474 0.000000 0.1960760 4.4245619
\(x_0\) -6.366519 29.913290 60.000000 -35.3621000 -13.0300715
\(y_0\) 56.836760 32.602280 18.077910 36.7704000 51.1796666
\(\theta_2^1\) 1.366547 6.283185 6.283185 1.6601500 5.9699819
\(\theta_2^2\) 2.330773 0.318205 0.264935 2.0468400 0.4554995
\(\theta_2^3\) 2.871039 0.638520 0.500377 2.4281100 1.0202707
\(\theta_2^4\) 3.394591 0.979950 0.735321 2.8090100 1.5550696
\(\theta_2^5\) 3.970960 1.412732 0.996529 3.1900900 2.1117409
\(\theta_2^6\) 4.963490 2.076254 1.333549 3.5737900 2.8839248
\(Error\) 0.002057 1.101697 0.122738 0.0000172 0.0000124

6.4.2 Case2 有规定时间的轨迹生成(with prescribed timing)

本案例四杆机构的路径为5个没有对齐的点（规定时间）。通过式(6.8)计算得到误差。

设计参数为：

\[ X = [r_1,r_2,r_3,r_4,r_p,\theta_p] \] 目标点坐标：

\[\begin{align} &\{C_d^i\} = \{(3,3),(2.759,3.363),(2.759,3.363),(1.890,3.862),(1.355,3.943)\} \notag \\ &\{\theta_2^1,\theta_2^2,\theta_2^3,\theta_2^4,\theta_2^5\}=\{\pi/6,\pi/4,\pi/3,5\pi/12,\pi/2\} \notag \\ \end{align}\]

参数约束：

\[ r_1,r_2,r_3,r_4\in[0,5]\quad r_p\in[-5,5]\quad \theta_p\in[0,2\pi] \]

算法参数为 \(d_0 = 0.10,\delta_0=0.05,c_1=0.9998,c_2=0.5,q=40,T_{max}=10000\)，动画结果如图6.5。

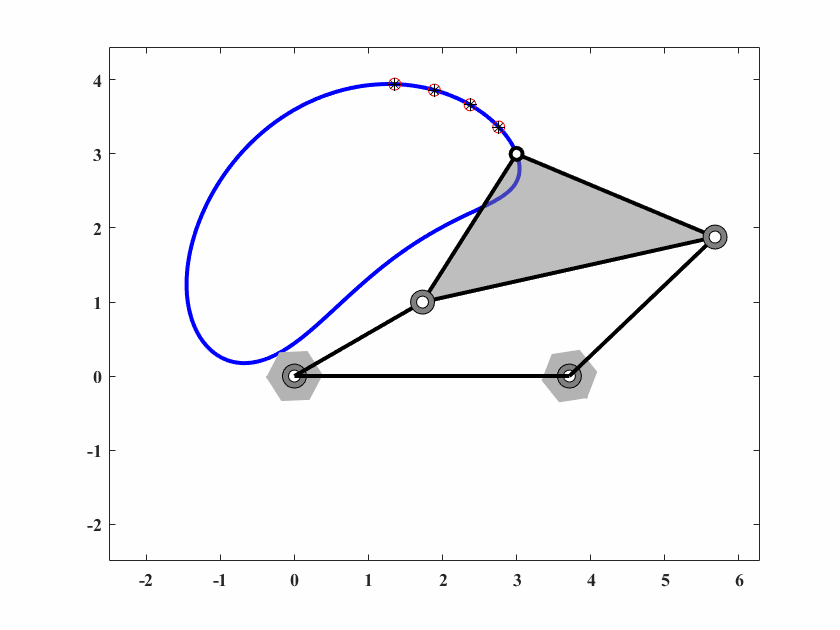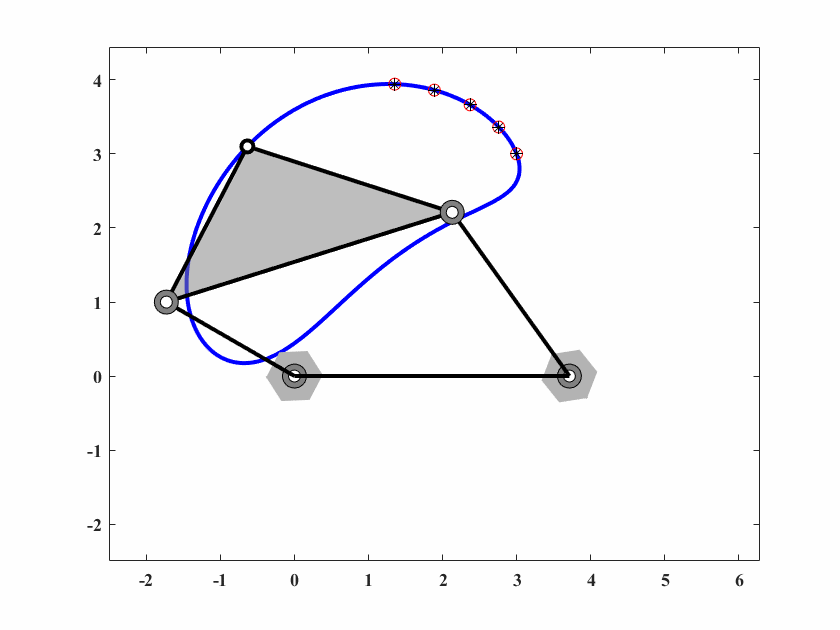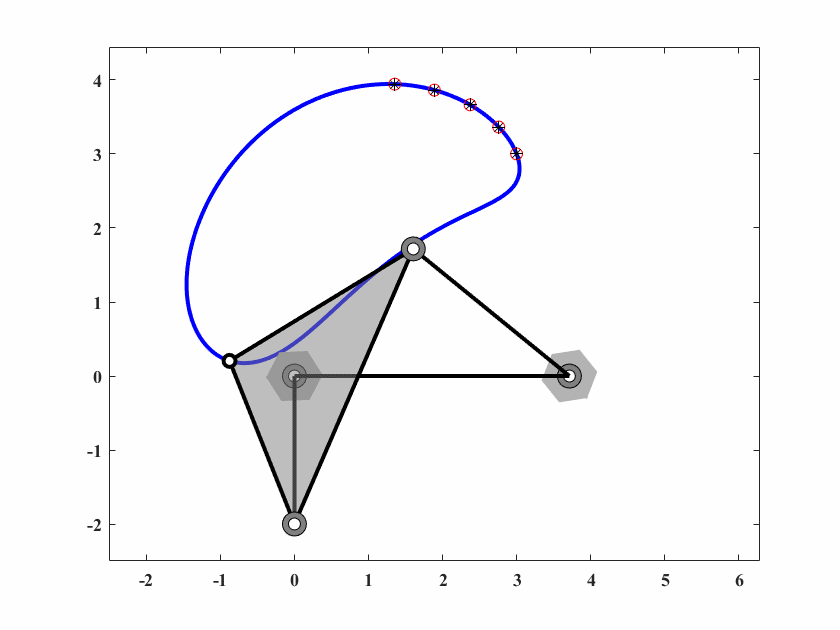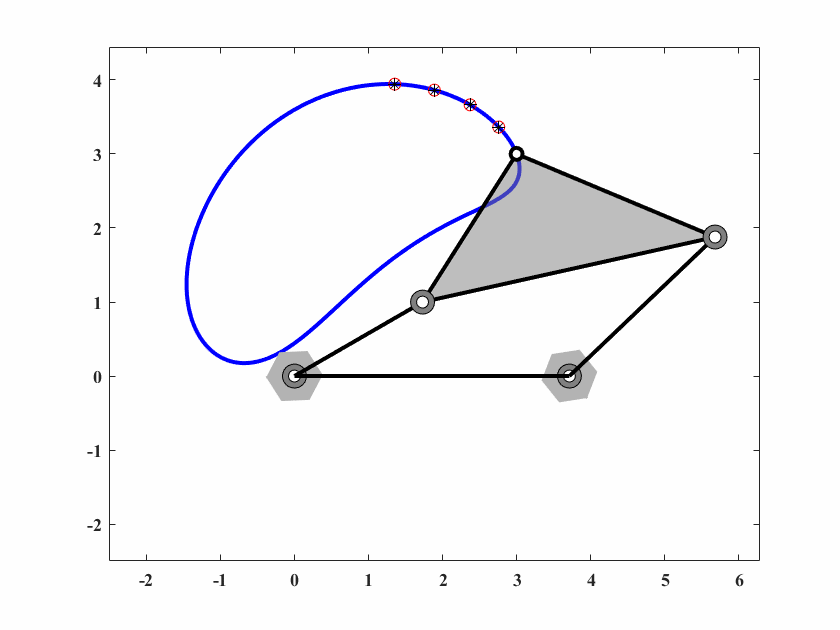
case2四杆机构轨迹生成

图 6.5: case2四杆机构轨迹生成

与其他算法对比结果如图6.6和表6.2。
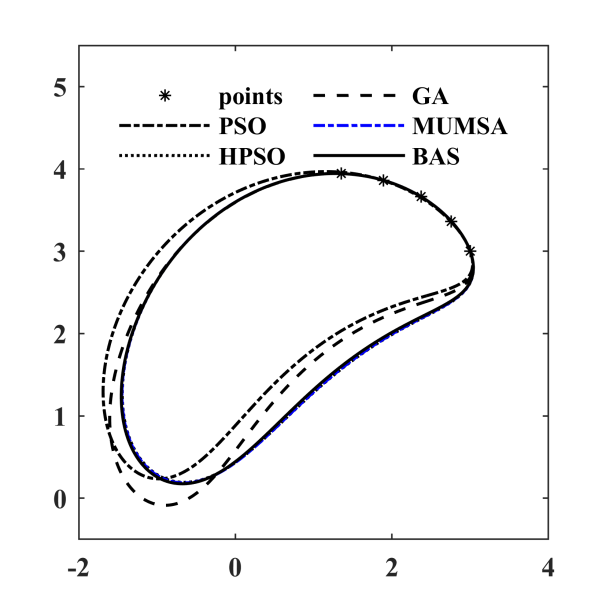
各算法优化轨迹

图 6.6: 各算法优化轨迹

表 6.2: case2各算法结果对比
PSO HPSO GA MUMSA BAS
\(r_1\) 3.0576200 3.7877200 3.0630424 3.7732686 3.7135255
\(r_2\) 1.8618400 1.9984200 1.9959624 2.0000040 1.9978745
\(r_3\) 3.8459100 4.1331300 3.3058230 4.1169710 4.0469527
\(r_4\) 2.9706300 2.7451300 2.5247060 2.7461567 2.7192391
\(r_p\) 2.4968270 2.3697220 2.3721479 2.3684374 2.3702974
\(\theta_p\) 0.7243557 0.7841479 0.8044176 0.7831567 0.7865371
\(Error\) 0.0005860 0.0009860 0.0000018 0.0000018 0.0000007

6.4.3 Case3 规定时间内路径生成（Path generation with prescribed timing）

本案例四杆机构需要在规定时间通过一个闭环。通过式(6.8)计算得到误差。

设计参数为：

\[ X = [r_1,r_2,r_3,r_4,r_p,\theta_p,\theta_0,x_0,y_0,\theta_2^1,\cdots,\theta_2^6] \]

目标点坐标：

\[\begin{align} \{C_d^i\} = \{&(0.5,1.1),(0.4,1.1),(0.3,1.1),(0.2,1.0),(0.1,0.9),(0.05,0.75), \notag \\ &(0.02,0.6),(0,0.5),(0,0.4),(0.03,0.3),(0.1,0.25),(0.15,0.2), \notag\\ &(0.2,0.3),(0.3,0.4),(0.4,0.5),(0.5,0.7),(0.6,0.9),(0.6,1.0)\} \notag\\ \{\theta_2^i\}=\{&\theta_2^1,\theta_2^1+20\cdot i/\pi\},\quad i = 1,\cdots,17 \notag \\ \end{align}\]

参数约束：

\[ r_1,r_2,r_3,r_4\in[0,5]\quad r_p,x_0,y_0\in[-5,5]\quad \theta_0,\theta_2^1,\theta_p\in[0,2\pi] \]

算法参数为 \(d_0 = 0.10,\delta_0=0.05,c_1=0.9998,c_2=0.5,q=8,T_{max}=50000\)，动画结果如图6.7。

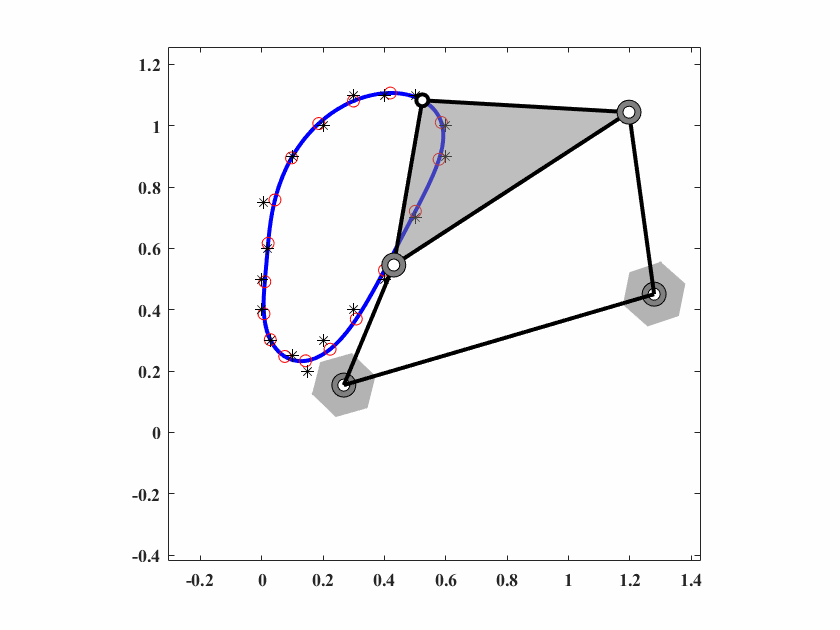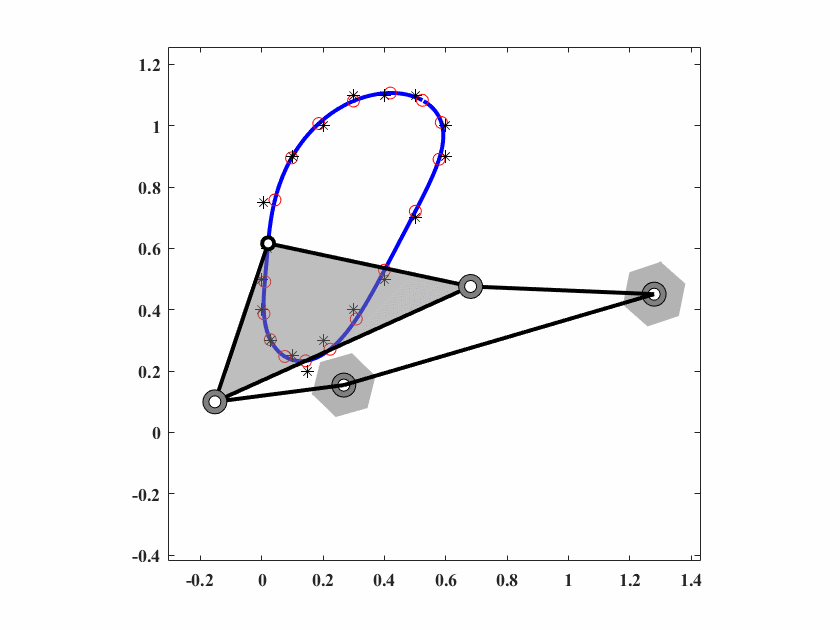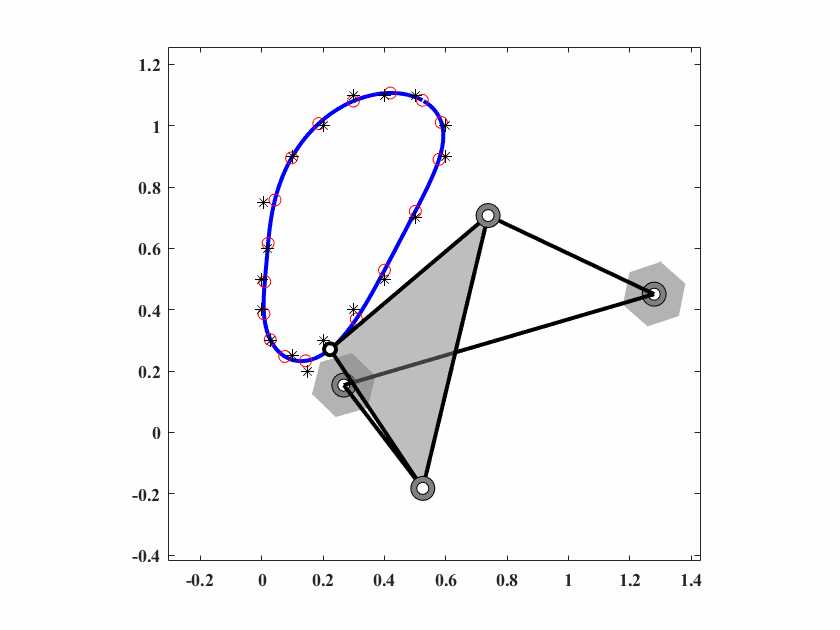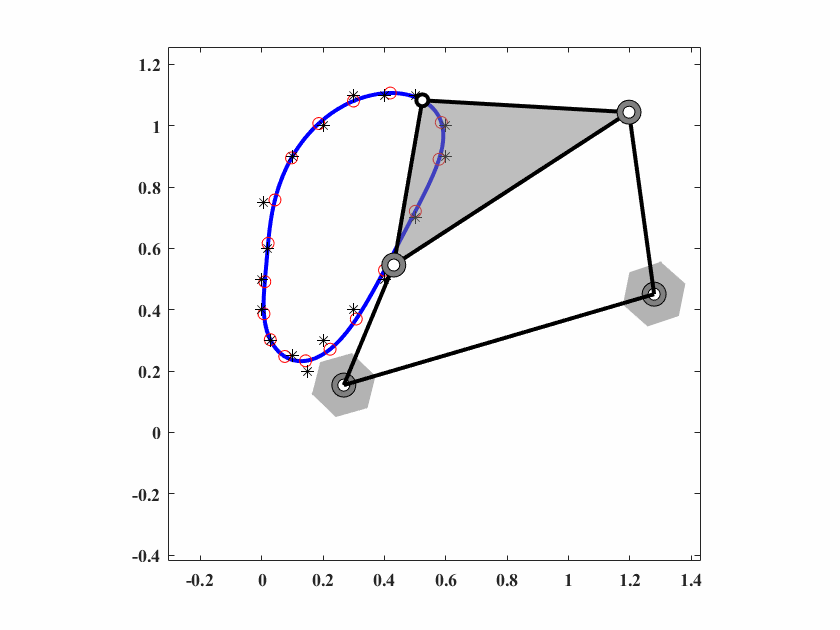
case3四杆机构轨迹生成

图 6.7: case3四杆机构轨迹生成

与其他算法对比结果如图6.8和表6.3。
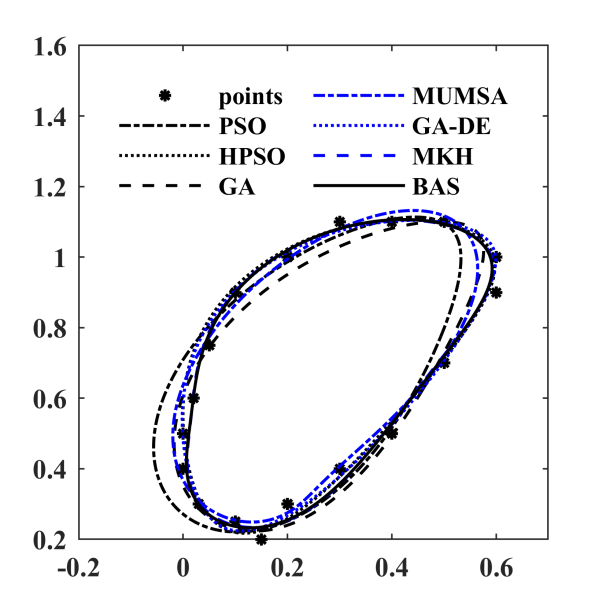
各算法优化轨迹

图 6.8: 各算法优化轨迹

表 6.3: case3各算法结果对比
PSO HPSO GA MUMSA GA.DE MKH BAS
\(r_1\) 2.9261 2.8500 3.0579 4.4538 47.4379 1.0043 1.0542
\(r_2\) 0.4877 0.3700 0.2378 0.2971 0.3248 0.4218 0.4239
\(r_3\) 2.9099 2.9048 4.8290 3.9131 0.4729 0.8782 0.9146
\(r_4\) 2.1503 0.5000 2.0565 0.8494 47.3093 0.5801 0.5989
\(r_p\) 1.4939 1.9737 2.0035 2.6520 0.3413 0.5234 0.5450
\(\theta_p\) -0.3325 1.0274 1.1779 2.4647 -1.2154 0.8148 0.8227
\(\theta_0\) 0.7190 0.7600 1.0022 2.7387 3.3203 0.2929 0.2850
\(x_0\) -0.3846 0.9400 1.7768 -1.3092 0.5270 0.2689 0.2677
\(y_0\) -0.6752 -1.1712 -0.6420 2.8070 0.7239 0.1772 0.1544
\(\theta_2^1\) 0.2159 0.5134 0.2262 4.8535 3.5123 0.8860 1.1764
\(Error\) 0.0492 0.0111 0.0337 0.0196 0.0109 0.0091 0.0090

6.4.4 Case4 规定时间路径生成问题

第四个案例同样是一个规定时间的路径生成问题。六个优化点由一个semi-archer弧构成，问题定义如下。

设计参数为：

\[ X = [r_1,r_2,r_3,r_4,r_p,\theta_p,\theta_0,x_0,y_0] \]

目标点坐标：

\[\begin{align} &\{C_d^i\} = \{(0,0),(1.9098,5.8779),(6.60989.5106),(13.09,9.5106),(18.09,5.8779),(20,0)\} \notag \\ &\{\theta_2^1,\theta_2^2,\theta_2^3,\theta_2^4,\theta_2^5\}=\{\pi/6,\pi/3,\pi/2,2\pi/3,5\pi/6,\pi\} \notag \\ \end{align}\]

参数约束：

\[ r_1,r_2,r_3,r_4\in[0,50]\quad r_p,x_0,y_0\in[-50,50]\quad \theta_0,\theta_p\in[0,2\pi] \]

算法参数为 \(d_0 = 0.10,\delta_0=0.05,c_1=0.9997,c_2=0.5,q=40,T_{max}=30000\)，动画结果如图6.9。

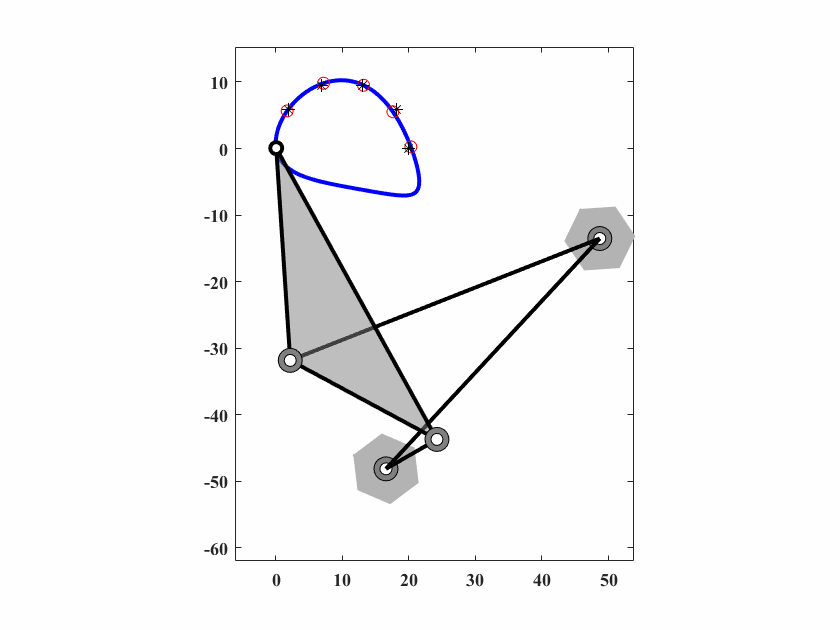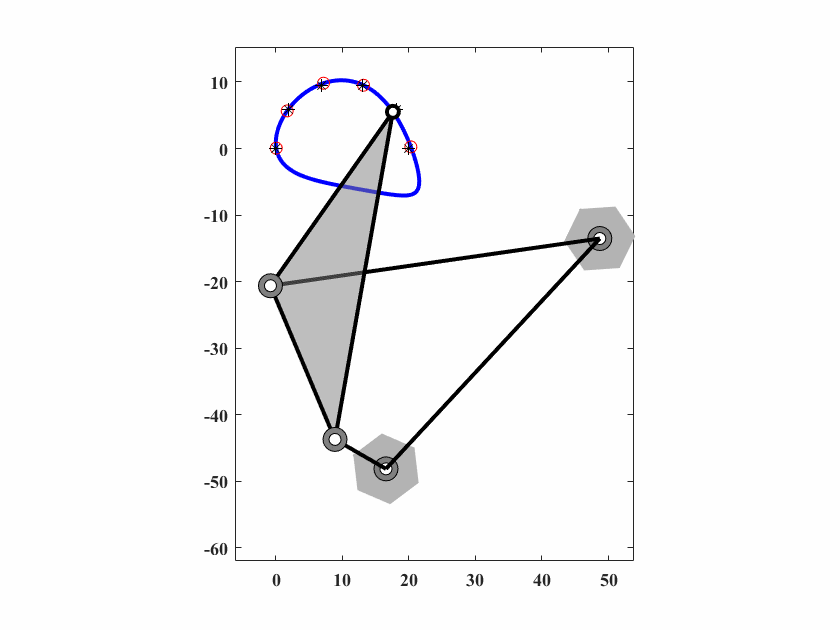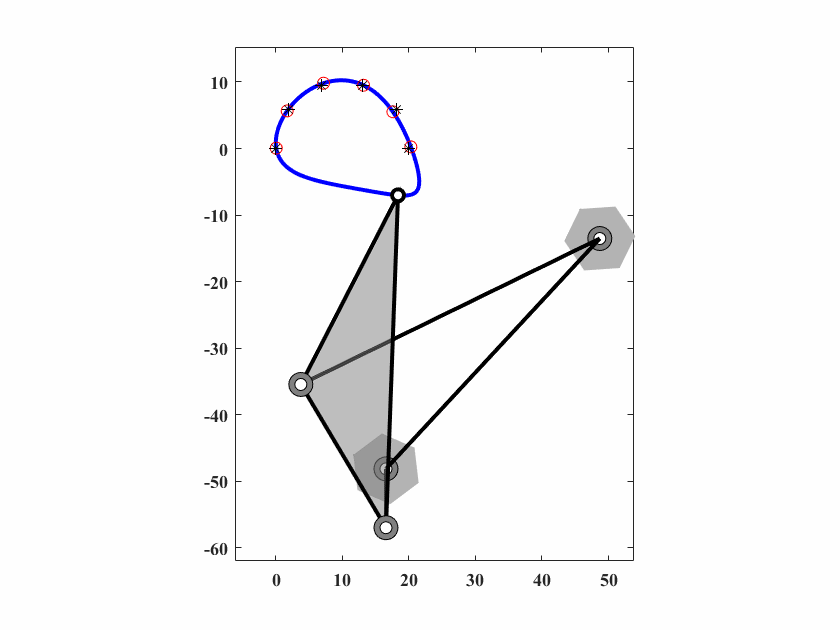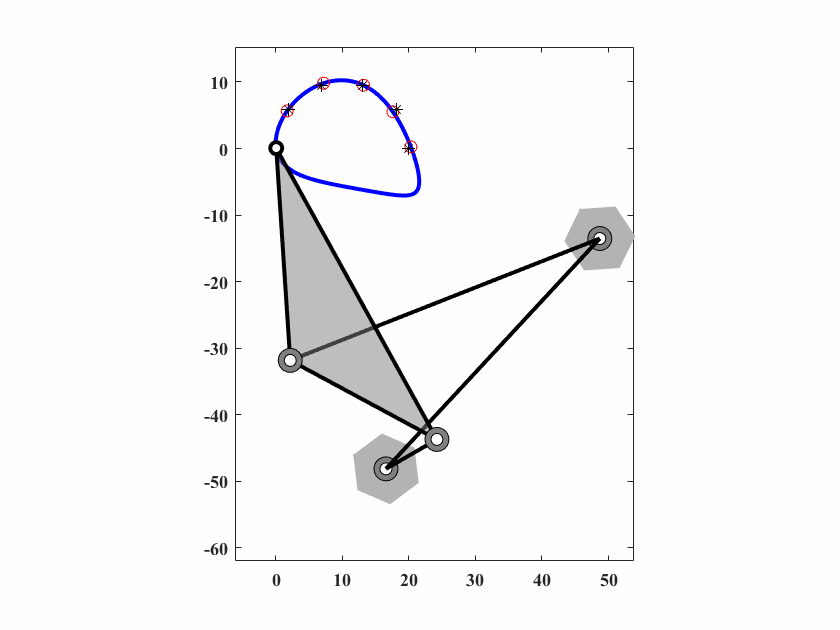
case4四杆机构轨迹生成

图 6.9: case4四杆机构轨迹生成

与其他算法对比结果如图6.10和表6.4。
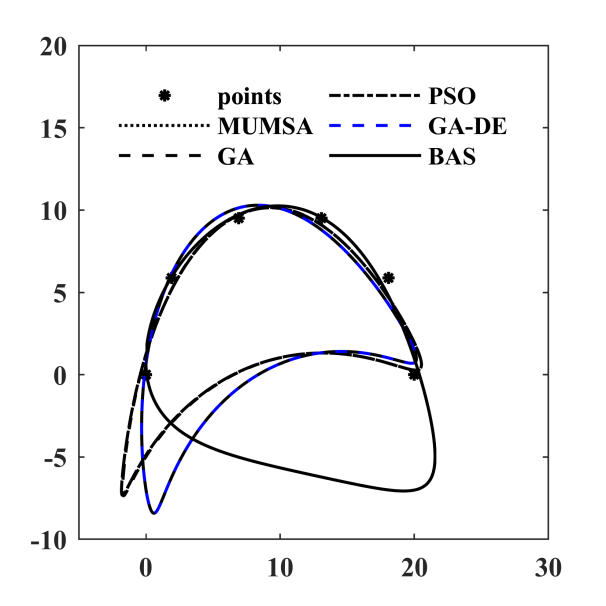
各算法优化轨迹

图 6.10: 各算法优化轨迹

表 6.4: case4各算法结果对比
MUMSA GA PSO GA.DE BAS
\(r_1\) 50.0000000 50.0000000 50.0000000 50.000000 47.2345017
\(r_2\) 5.0000000 5.0000000 5.0000000 5.000000 8.8473992
\(r_3\) 7.0310470 6.9700900 7.0310200 5.905343 25.0474709
\(r_4\) 48.1341830 48.1993000 48.1342000 50.000000 50.0000000
\(r_p\) 21.3533558 21.2191204 21.3532819 18.819312 50.0000000
\(\theta_p\) 0.6517294 0.6380060 0.6517238 0.000000 5.7107187
\(\theta_0\) 0.0428247 0.0508453 0.0428286 0.463633 0.8225945
\(x_0\) 12.1974940 12.2377000 12.1975000 14.373772 16.5531171
\(y_0\) -15.9982030 -15.8332000 -15.9981000 -12.444295 -48.1473786
\(Error\) 2.5803500 2.5828600 2.5803600 2.349649 0.7863680

6.4.5 Case5 规定时间内路径生成问题

这个例子是一个椭圆路径生成问题，没有规定的时间，其中轨迹是由10个点定义的。问题定义如下。

设计参数为：

\[ X = [r_1,r_2,r_3,r_4,r_p,\theta_p,\theta_0,x_0,y_0,\theta_2^1,\cdots,\theta_2^{10}] \]

目标点坐标：

\[\begin{align} \{C_d^i\} = \{&(20,10),(17.66,15.142),(11.736,17.878),(5,16.928),(0.60307,12.736), \notag \\ &(0.60307,7.2638),(5,3.0718),(11.736,2.1215),(17.66,4.8577),(20,0)\}\notag\\ \end{align}\]

参数约束：

\[ r_1,r_2,r_3,r_4\in[0,80]\quad r_p,x_0,y_0\in[-80,80]\quad \theta_0,\theta_2^1,\cdots,\theta_2^{10},\theta_p\in[0,2\pi] \]

算法参数为 \(d_0 = 0.10,\delta_0=0.05,c_1=0.9998,c_2=0.5,q=40,T_{max}=40000\)，动画结果如图6.11。

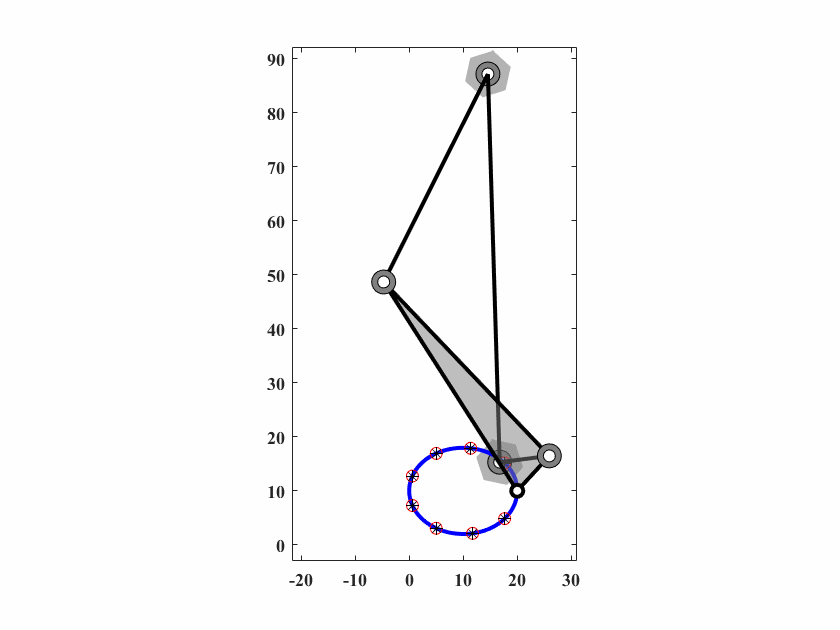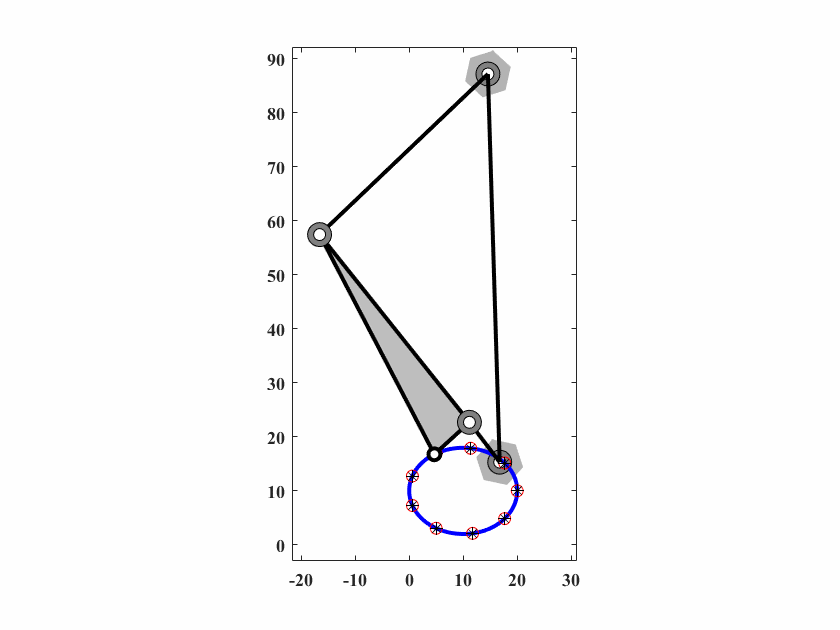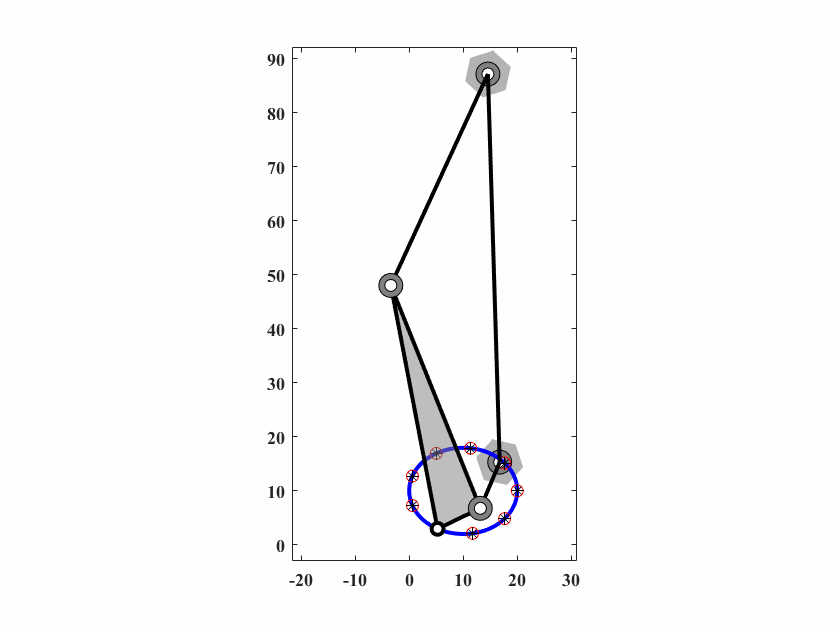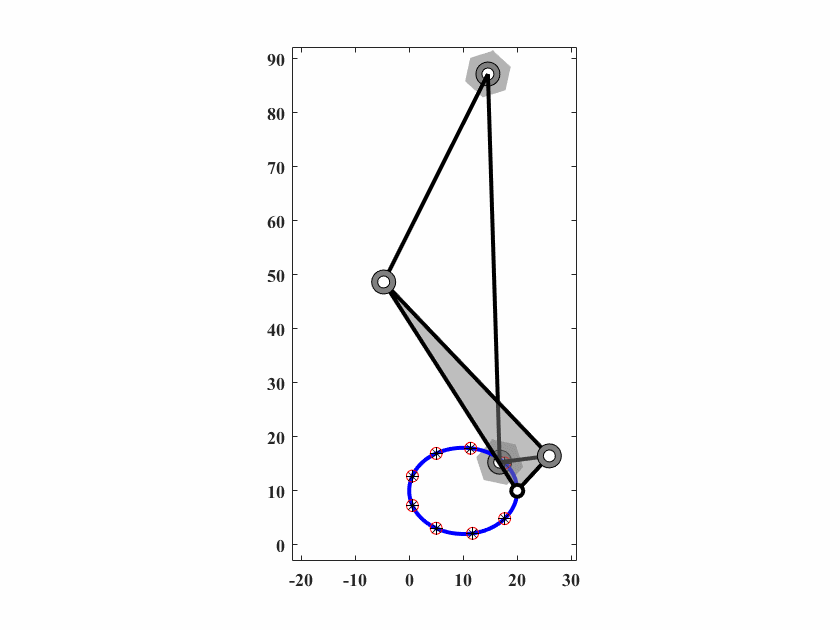
case5四杆机构轨迹生成

图 6.11: case5四杆机构轨迹生成

与其他算法对比结果如图6.12和表6.5。
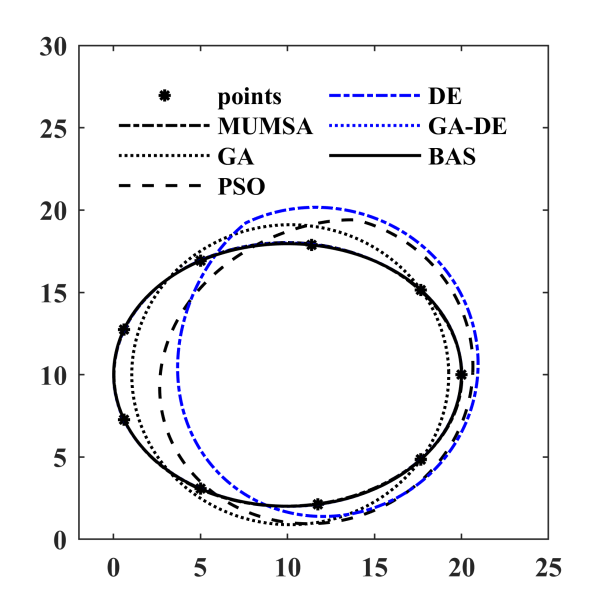
各算法优化轨迹

图 6.12: 各算法优化轨迹

表 6.5: case5各算法结果对比
MUMSA GA PSO DE GA.DE BAS
\(r_1\) 79.5160680 79.981513 52.535162 54.360893 80.0000000 71.8681225
\(r_2\) 9.7239730 9.109993 8.687886 8.683351 8.4203200 9.2618623
\(r_3\) 45.8425240 72.936511 36.155078 34.318634 51.3426000 44.4542963
\(r_4\) 51.4384800 80.000000 80.000000 79.996171 42.4532000 43.0533508
\(r_p\) 8.7289390 0.000000 1.481055 1.465250 10.6530404 8.7820722
\(\theta_p\) -0.3452264 0.000000 1.570796 1.570669 2.6465448 1.6362575
\(\theta_0\) 5.5969445 0.026149 1.403504 2.129650 4.2817700 1.6011655
\(x_0\) 2.0211090 10.155966 11.002124 10.954397 5.5337200 16.7540360
\(y_0\) 13.2165878 10.000000 11.095585 11.074534 0.4771830 15.2986682
\(\theta_2^1\) 0.6376873 6.283185 6.282619 6.283185 2.0935000 0.1258416
\(\theta_2^2\) 1.3255329 0.600745 0.615302 0.616731 2.8129100 0.8167208
\(\theta_2^3\) 2.0080339 1.372812 1.305421 1.310254 3.5160500 1.5351326
\(\theta_2^4\) 2.6955659 2.210575 2.188053 2.193570 4.2063800 2.1811489
\(\theta_2^5\) 3.3845794 2.862639 2.913049 2.917170 4.8905100 2.8753839
\(\theta_2^6\) 4.0829376 3.420547 3.499313 3.490746 5.5739800 3.5728072
\(\theta_2^7\) 4.7984548 4.072611 4.125586 4.132017 6.2645800 4.2854058
\(\theta_2^8\) 5.5117056 4.910373 4.919977 4.922075 0.6761980 5.0016208
\(\theta_2^9\) 6.2127919 5.682440 5.685021 5.695372 1.3830700 5.7133417
\(\theta_2^{10}\) 0.6371866 6.283185 6.282323 6.282970 2.0934800 0.1258290
\(Error\) 0.0047000 2.281273 1.971004 1.952326 0.0006022 0.0004252

6.4.6 Case6 六杆机构路径生成

这个案例我也看不懂。大概意思是，六杆问题，在规定时间内让轨迹耦合目标点，并且output link在停顿位置（dwell portion?我翻译不下去了……）保持在一个精确的角度。大家看底下的原文靠谱一点。

“This case is a path and function combined synthesis problem with prescribed timing in which the coupler of six-bar mechanism has to the precision points and its output link has to maintain an accuracy angle in the dwell portion.”

— Xiaojuan Mo

设计参数为：

\[ X = [r_1,r_2,r_3,r_4,r_5,r_6,r_p,\theta_p,r_1',\theta_0,\theta_0',x_0,y_0,\theta_2^1] \]

目标点坐标：

\[\begin{align} \{C_d^i\} = \{&(-0.5424,2.3708),(0.2202,2.9871),(0.9761,3.4633), \notag \\ &(1.0618,36380),(0.8835,3.7226),(0.5629,3.7156),\notag \\ &(0.1744,3.6128),(-0.2338,3.4206),(-0.6315,3.1536), \notag \\ &(-1.0,2.8284),(-1.3251,2.4600),(-1.5922,2.0622), \notag \\ &(-1.7844,1.6539),(-1.8872,1.2654),(-1.8942,0.9448), \notag \\ &(-1.8096,0.7665),(-1.6349,0.8522),(-1.1587,1.6081)\} \notag \\ \{\theta_2^i\} = \{&0,15,40,60,80,100,120,140,160,180,\notag \\ & 200, 220,240,260,280,300,320,345\} \notag \\ & \rightarrow \theta_2^i = \theta_2 + \delta_2^i \notag \\ \end{align}\]

在停顿位置处的输入输出角度的关联如下：

\[\begin{align} &\theta_2^i = \theta_2^1+\{160,180,200,220\}\rightarrow \theta_6^i=210 \notag \\ &\theta_2^i=\theta_2^1+\{345,0,15\} \rightarrow \theta_6^i = 225 \notag \\ \end{align}\]

注意，上述涉及到角度的数值单位均为deg，而非弧度。

算法参数为 \(d_0 = 0.05,\delta_0=0.025,c_1=0.9999,c_2=0.5,q=10,T_{max}=50000\)，动画结果如图6.13。

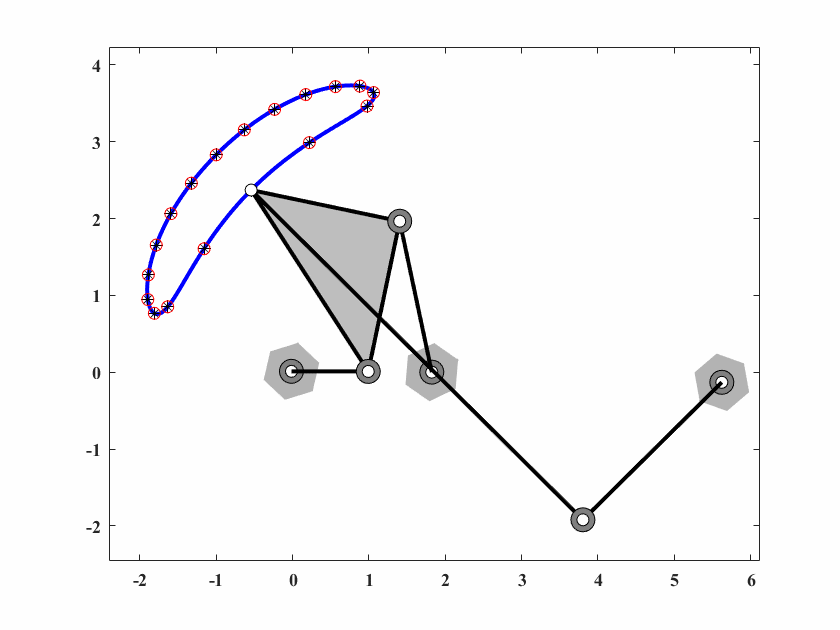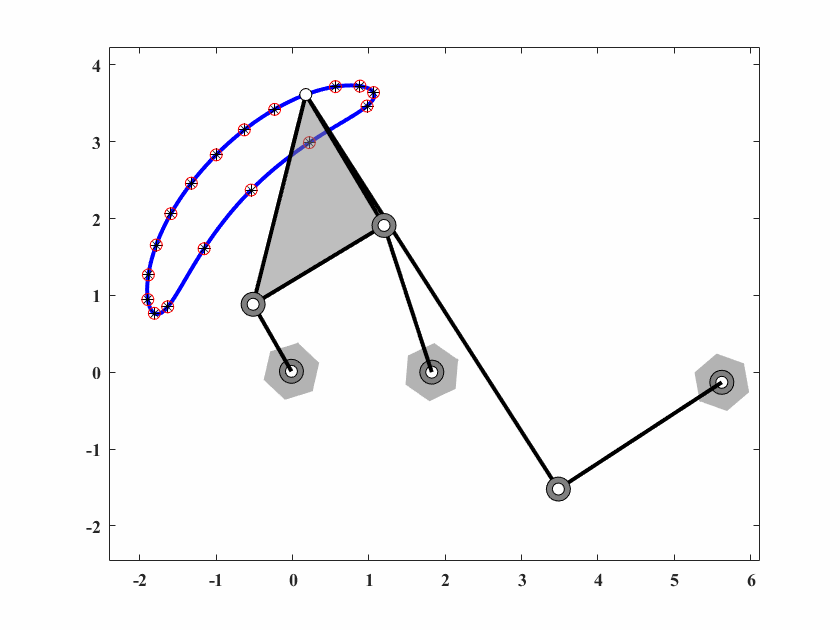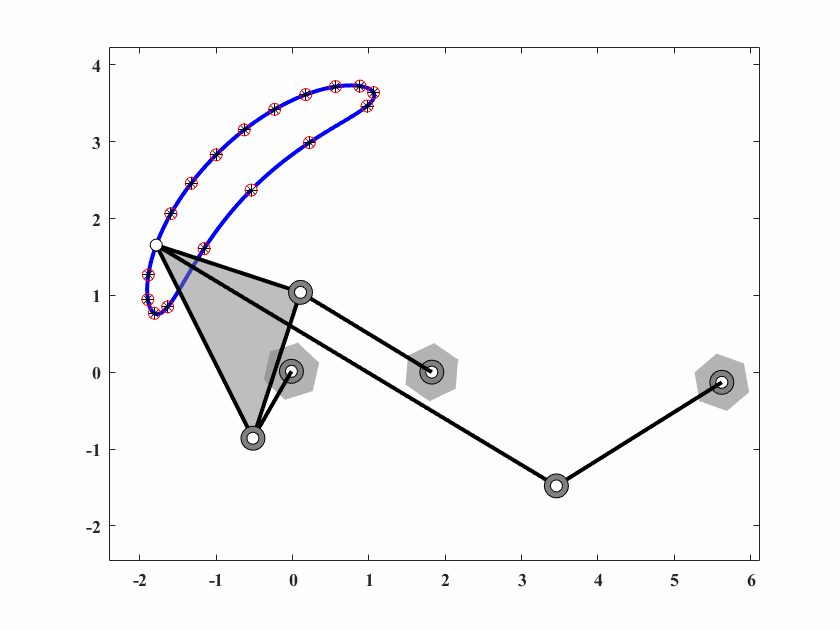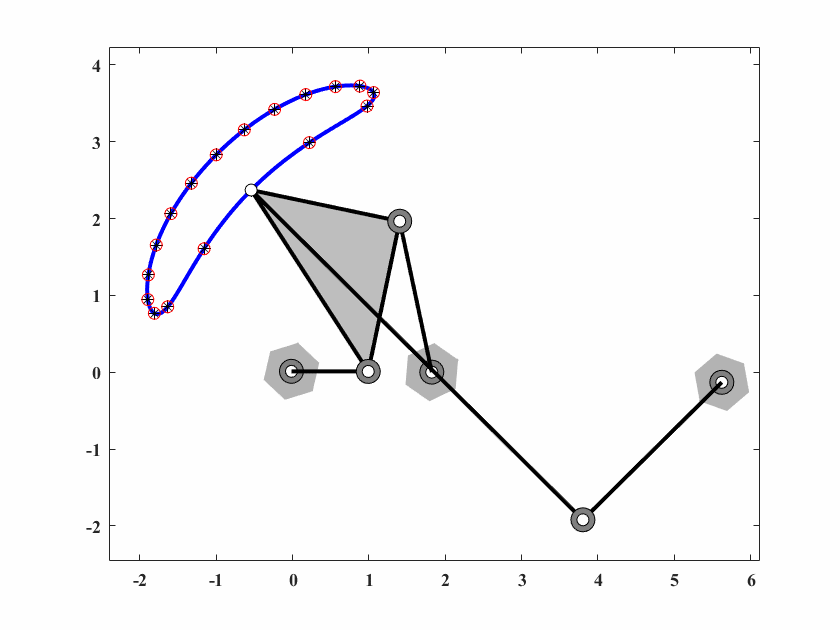
case6六杆机构轨迹生成

图 6.13: case6六杆机构轨迹生成

与其他算法对比结果如图6.14, 图6.15和表6.6。

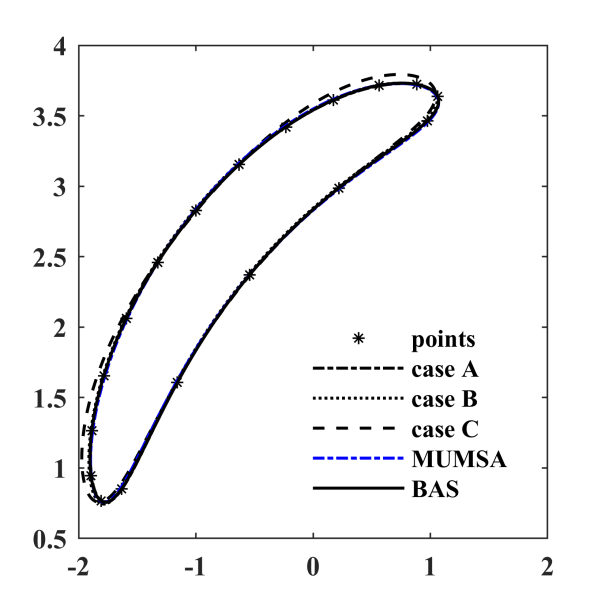
各算法优化轨迹

图 6.14: 各算法优化轨迹

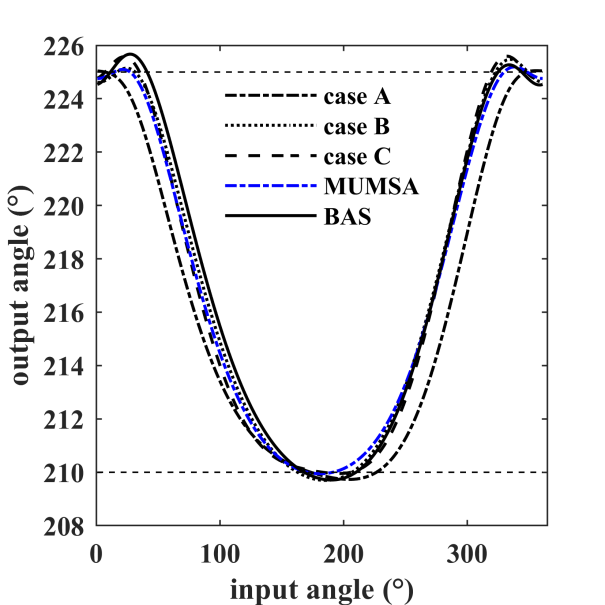
各算法优化角度

图 6.15: 各算法优化角度

表 6.6: case6各算法结果对比
DE.A DE.B DE.C MUMSA BAS
\(r_1\) 1.8145 1.8065 2.0926 1.713529 1.838058488
\(r_2\) 0.9911 0.9826 1.1464 0.92602 1.006097698
\(r_3\) 1.9995 2.0177 1.989 1.991373 1.997800646
\(r_4\) 2.0315 2.0009 1.9727 1.848672 2.008472163
\(r_5\) 4.3674 5.7769 6.6633 5.35498 6.106586728
\(r_6\) 2.4924 2.5296 2.5517 2.54979 2.551492193
\(r_p\) 2.8174 2.8711 2.7178 2.975936132 2.815041279
\(\theta_p\) 0.7776 0.783712 0.845246 0.831651258 0.78386985
\(\theta_0\) 6.269879 0.011582 6.242260827 0.067677 6.277427755
\(r_1'\) 4.4158 5.2817 6.2907 4.87374 5.63828226
\(\theta_0'\) 0.235595 0.0170309 6.18118303 0.0967027 6.257863894
\(x_0\) 0.0115 0.0415 -0.2729 0.175257 -0.013849346
\(y_0\) 0.0157 -0.0377 0.0931 -0.1187032 0.011591976
\(\theta_2^1\) 0.00052 0.003648 -0.04062 6.222361 6.281768246
\(Evaluations\) 53310 93405 93405 93405 50000
\(Error\) 0.000250876 0.005653158 0.03537533 0.0014 0.000195212659

6.4.7 Case7 无规定时间的路径生成

本案例为一个’8’型路径生成问题，轨迹由12个点规定。

设计参数为：

\[ X = [r_1,r_2,r_3,r_4,r_p,\theta_p,\theta_0,x_0,y_0,\theta_2^1,\cdots,\theta_2^{12}] \]

目标点坐标：

\[\begin{align} \{C_d^i\} = \{&(4.15,2.21),(4.50,2.18),(4.53,1.83),(4.13,1.68),(3.67,1.58),(2.96,1.33), \notag \\ &(2.67,1.06),(2.63,0.82),(2.92,0.81),(3.23,1.07),(3.49,1.45),(3.76,1.87)\}\notag\\ \end{align}\]

参数约束：

\[\begin{align} &r_1\in[0,5]\quad r_2,r_3,r_4\in[0,10] \quad r_p\in[0,14],\notag \\ &x_0,y_0\in[-80,80]\quad \theta_0,\theta_2^1,\cdots,\theta_2^{12},\theta_p\in[0,2\pi] \notag \\ \end{align}\]

算法参数为 \(d_0 = 0.05,\delta_0=0.025,c_1=0.9995,c_2=0.5,q=40,T_{max}=20000\)，动画结果如图6.16。

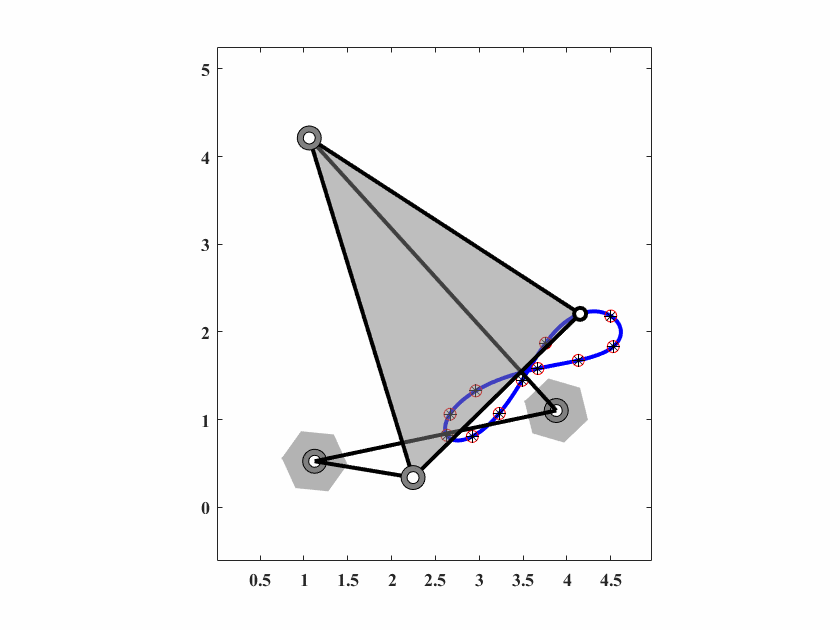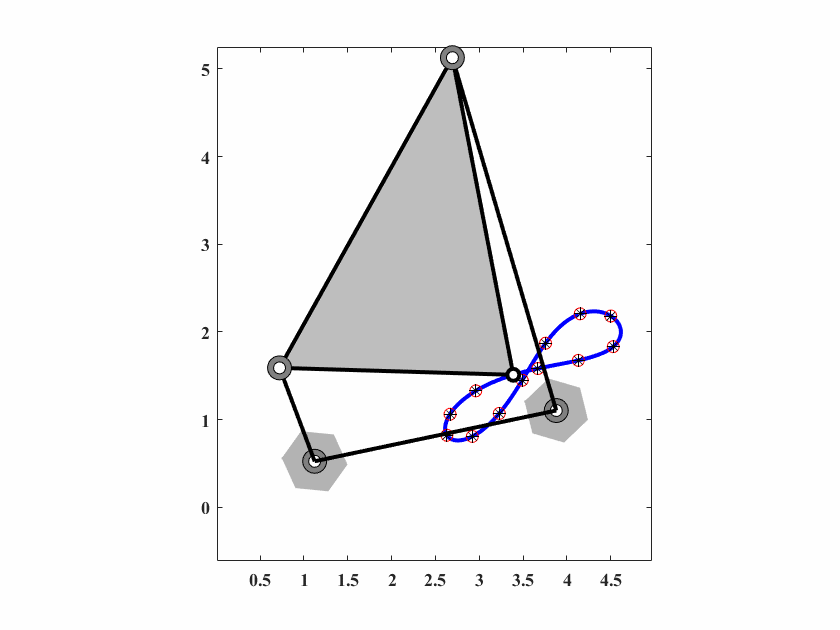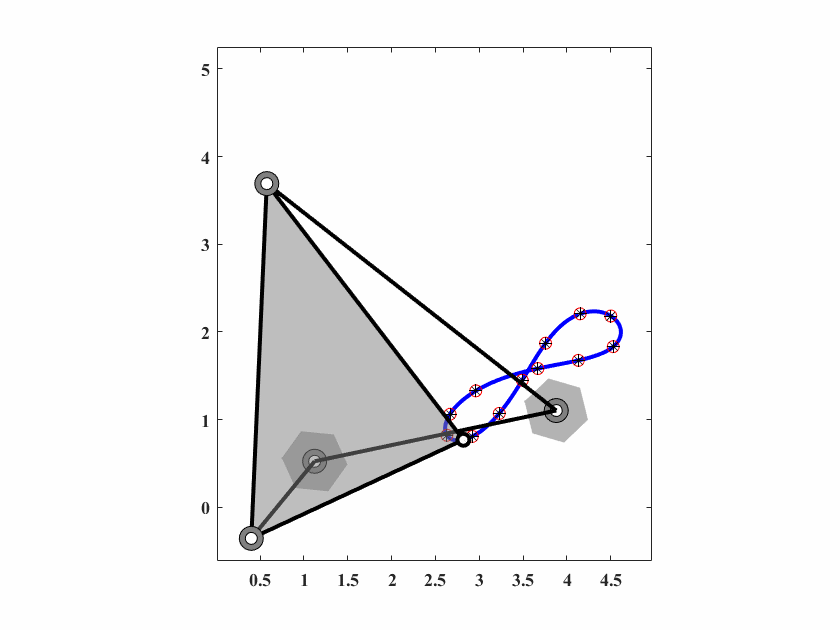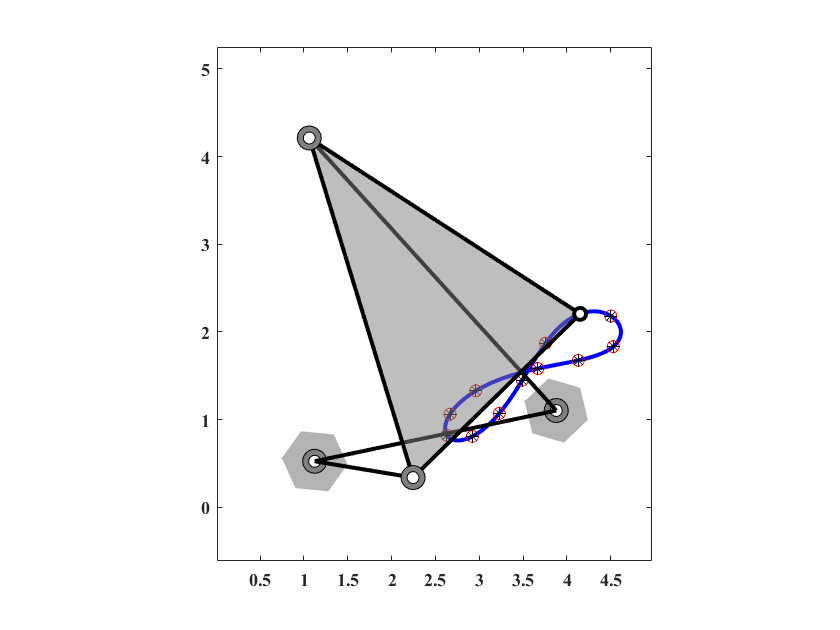
case7机构轨迹生成

图 6.16: case7机构轨迹生成

与其他算法对比结果如图6.17和表6.7。
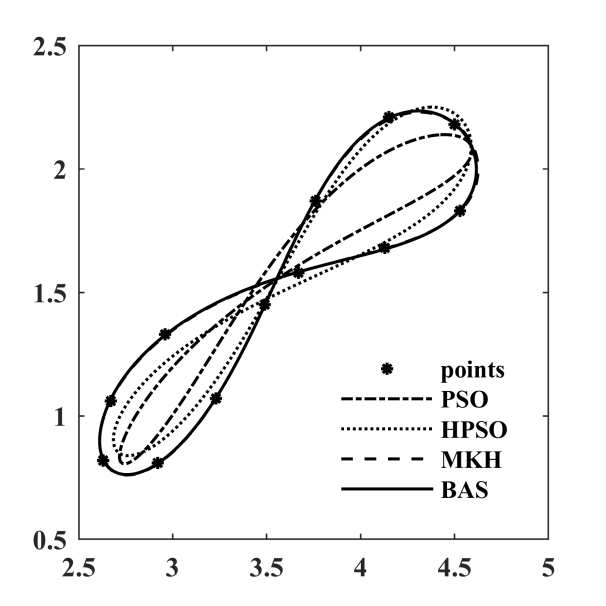
各算法优化轨迹

图 6.17: 各算法优化轨迹

表 6.7: case7各算法结果对比
PSO HPSO MKH BAS
\(r_1\) 4.550300 4.535900 2.8764500 2.8162769
\(r_2\) 1.101300 1.113300 1.1464400 1.1382629
\(r_3\) 3.955800 14.738100 4.4077300 4.0509922
\(r_4\) 3.933000 16.801700 4.7571300 4.1957758
\(r_p\) 3.941572 3.941866 2.6665746 2.6682801
\(\theta_p\) -0.539171 -1.521104 -1.1363513 5.1910788
\(\theta_0\) 0.000000 0.000000 0.1650200 0.2070603
\(x_0\) 0.000000 0.000000 1.1426500 1.1226995
\(y_0\) 0.000000 0.000000 0.4823700 0.5246662
\(\theta_2^1\) -0.201400 -0.181600 -0.3139900 6.1191060
\(Error\) 0.171600 0.096400 0.0001597 0.0000994

6.4.8 Case8 无规定时间的路径生成

本案例为一个叶形路径生成问题（无规定时间），轨迹由25个点规定。

设计参数为：

\[ X = [r_1,r_2,r_3,r_4,r_p,\theta_p,\theta_0,x_0,y_0,\theta_2^1,\cdots,\theta_2^{25}] \]

目标点坐标：

\[\begin{align} \{C_d^i\} = \{&(7.03,5.99),(6.95,5.45),(6.77,5.03),(6.4,4.6),(5.91,4.03), \notag \\ &(5.43,3.56),(4.93,2.94),(4.67,2.6),(4.38,2.2),(4.04,1.67),\notag \\ &(3.76,1.22),(3.76,1.97),(3.76,2.78),(3.76,3.56),(3.76,4.34), \notag \\ &(3.76,4.91),(3.76,5.47),(3.8,5.98),(4.07,6.4),(4.53,6.75), \notag \\ &(5.07,6.85),(5.05,6.84),(5.89,6.83),(6.41,6.8),(6.92,6.58)\} \notag \\ \end{align}\]

参数约束：

\[ r_1,r_2,r_3,r_4\in[0,5]\quad r_p,x_0,y_0\in[-5,5] \quad \theta_0,\theta_2^1,\cdots,\theta_2^{25},\theta_p\in[0,2\pi] \]

算法参数为 \(d_0 = 0.05,\delta_0=0.025,c_1=0.99975,c_2=0.5,q=40,T_{max}=50000\)，动画结果如图6.18。

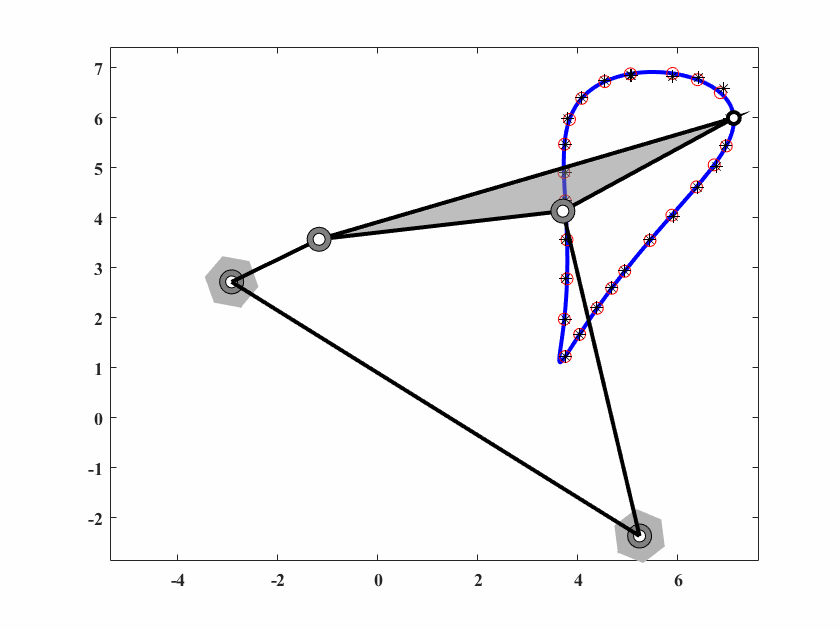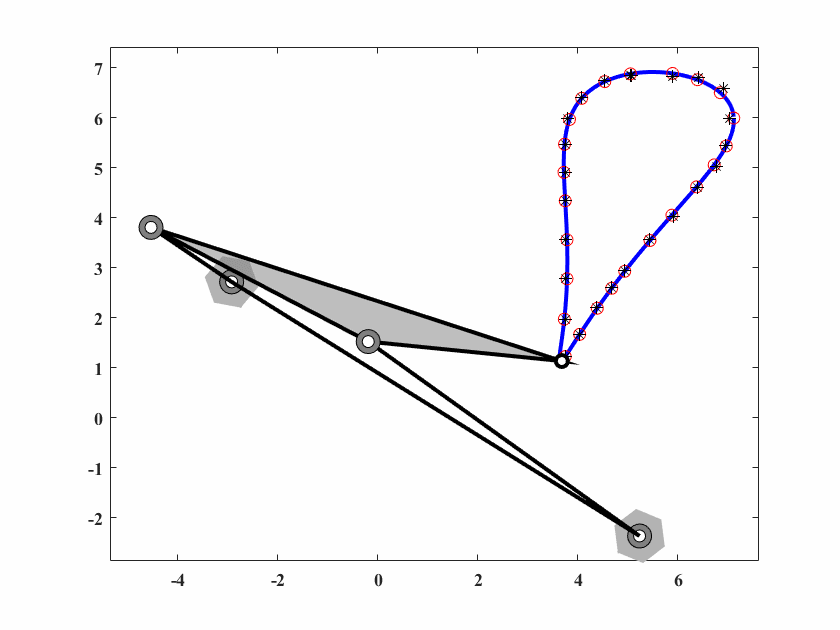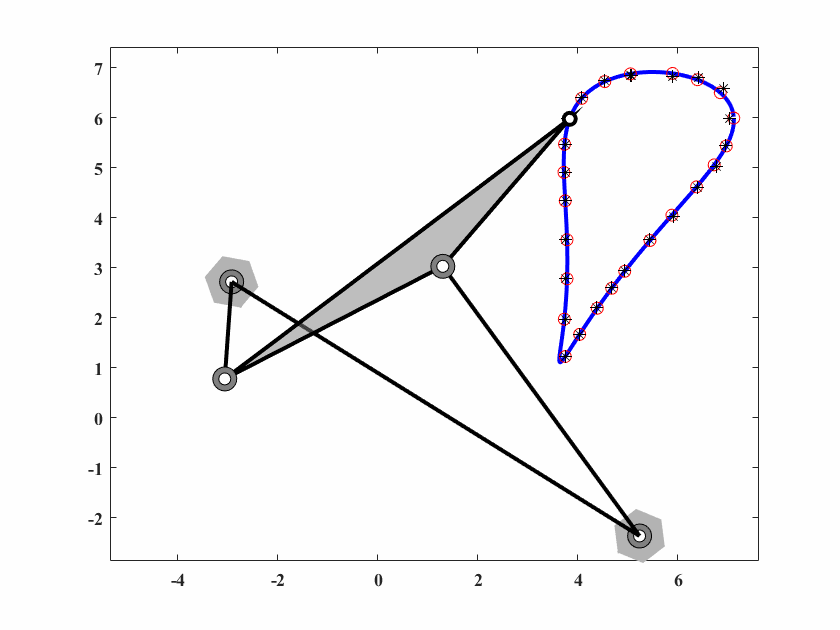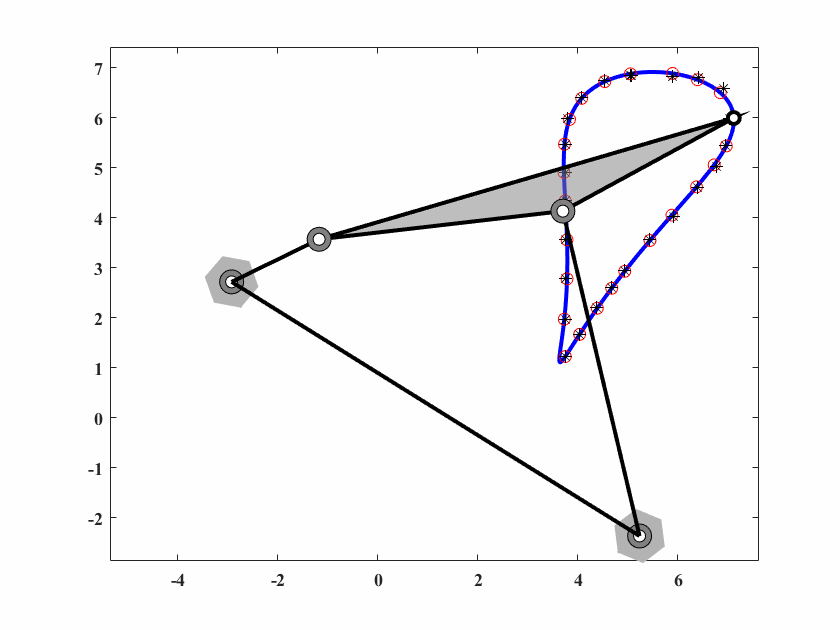
case8机构轨迹生成

图 6.18: case8机构轨迹生成

与其他算法对比结果如图6.19和表6.8。
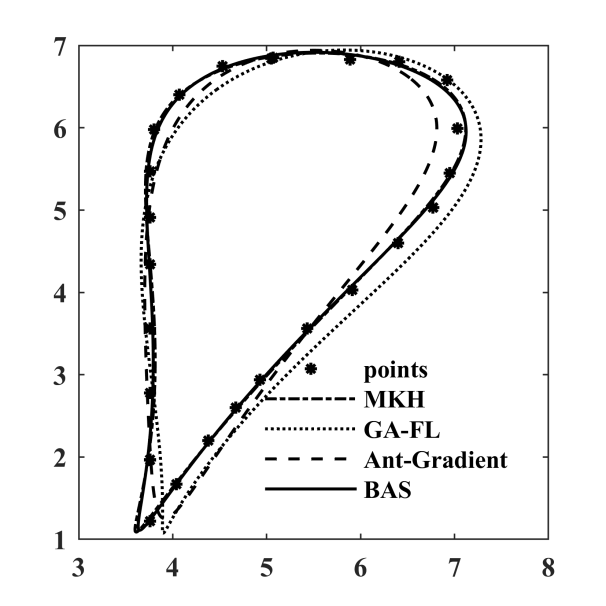
各算法优化轨迹

图 6.19: 各算法优化轨迹

表 6.8: case8各算法结果对比
MKH GA.FL Ant.Gradient BAS
\(r_1\) 9.99432 9 13.08 9.6132193
\(r_2\) 1.93027 3.01 1.89 1.9459840
\(r_3\) 4.57242 8.8 8.41 4.9080817
\(r_4\) 7.36674 8.8 6.75 6.6768279
\(r_p\) 8.04254 11.0995 14.45 8.6409226
\(\theta_p\) 0.187430 -0.681 0.195 0.1694076
\(\theta_0\) -0.61763 0.489 -0.3815 5.7260733
\(x_0\) -2.31301 -2.4 -8.77 -2.9214626
\(y_0\) 2.86189 -4 1.20 2.7190256
\(\theta_2^1\) * * * 0.4529787
\(Error\) 0.03916 0.9022 0.5504 0.0397777